Friction and torque of ladder resting on wall

[SA32]

Homework Statement

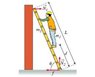
A uniform ladder with mass m₂ and length L rests against a smooth wall. A do-it-yourself enthusiast of mass m₁ stands on the ladder a distance d from the bottom (measured along the ladder). The ladder makes an angle x with the ground. There is no friction between the wall and the ladder, but there is a frictional force of magnitude f between the floor and the ladder. N₁ is the magnitude of the normal force exerted by the wall on the ladder, and N₂ is the magnitude of the normal force exerted by the ground on the ladder. Throughout the problem, consider counterclockwise torques to be positive. None of your answers should involve pi (i.e., simplify your trig functions).

Sum the torques given in the problem about the point at which the ladder touches the wall.

Homework Equations

T(torque)=F*d

See attachment for diagram.

The Attempt at a Solution

I know the answer is,

-m₁g(L-d)cos(x)-(m₂g)(L/2)(cos(x))-fLsin(x)+N₂Lcos(x)

I know that torque is the force multiplied by the distance to the pivot point. What I don't get is why we are only concerned with with each force's vertical distance from the pivot point and not the horizontal distance. Help, please?

 

[Doc Al]

I know that torque is the force multiplied by the distance to the pivot point.

Actually, torque is the force multiplied by the perpendicular distance to the pivot point--direction matters!

What I don't get is why we are only concerned with with each force's vertical distance from the pivot point and not the horizontal distance.

Since it's the perpendicular distance that counts: for vertical forces (like weight and normal force), it's the horizontal distance; but for horizontal forces (like friction), it's the vertical distance.

 

[SA32]

Ahh, that makes sense. Thanks!