Friction Problem - block on an incline (serway)

[aero_zeppelin]

Hi, I've been trying to nail this problem but I'm not sure if I'm stating it correctly:

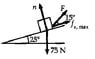
1. "A block weighing 75.0 N rests on a plane inclined at 25.0° to the horizontal. A force F is applied to the object at 40.0° to the horizontal, pushing it upward on the plane. The coefficients of static and kinetic friction between the block and the plane are, respectively, 0.363 and 0.156. (a) What is the minimum value of F that will prevent the block from slipping down the plane?"

Homework Equations

Regarding the first question "a", this is what I have stated:

Ʃ Fx = Fsin15° + fs - (75 sin 25°) = 0
Ʃ Fy = n - ( 75 N cos 25°) + F cos 15° = 0

Having n= normal force , fs = static friction = (μs)(n) , μs = coefficient of static friction, and remembering the incline is the x-axis (using sin for it) and the y-axis perpendicular to it (using cos).

The Attempt at a Solution

From ƩFy , we get n = ( 75 N cos 25°) - F cos 15°

Then from ƩFx, we get fs = (75 sin 25°) - Fsin15°

Considering fs = (μs)(n), we substitute and get:
(μs)(n) = (75 sin 25°) - Fsin15° and then we substitute n and get:

(μs) ( 75 N cos 25° - F cos 15°) = (75 sin 25°) - Fsin15°

Solving for F I get F = 40 N or something, but the book says it's F= 8.05 N.

Maybe I'm stating the sum of forces above wrong... Please help! Thx!

 

[PhanthomJay]

You are summing forces nicely, but you sined when you should have cosined, and v.v., when calculating the horiz and vert components of F.

 

[PICsmith]

Ʃ Fx = Fsin15° + fs - (75 sin 25°) = 0
Ʃ Fy = n - ( 75 N cos 25°) + F cos 15° = 0

Hi aero_zeppelin, I think you've got some trig mistakes in your initial equations. Specifically, check your Fsin15° and Fcos15° terms.

EDIT: Yeah, what PhanthomJay said. Also, I think it helps with trig mistakes to always take your angles w.r.t. the same axis (x-axis in this case). Then all your x-terms will have cosines and y-terms sines.

 

[aero_zeppelin]

lol, yeah, that's what I said, but the book recommends using that kind of axes when working with inclines. Actually, I've been working other similar problems with that method and I've gotten correct results. Don't know what the mistake is here...

Ok, so I changed the cos and sin to their "usual" axes and got F = 70.5 N XD

Any other idea?? thanks for the help!

 

[PICsmith]

lol, yeah, that's what I said, but the book recommends using that kind of axes when working with inclines.

No no, I meant that the x-axis should be defined parallel to the incline, along the direction of motion, as you did initially, but that you should take your angles w.r.t. that axis. You took a couple angles w.r.t. the y-axis (perpendicular to the incline), which isn't wrong, but mistakes are easier to make that way I think.

I ran the numbers using the following equations and I'm getting 8.05 N just like your book says it should be.
\sum F_x = F\cos 15^{\circ} - 75\cos 65^{\circ} + \mu F_N = 0
\sum F_y = F\sin 15^{\circ} - 75\sin 65^{\circ} + F_N = 0
Your procedure is right: just solve one equation for the normal force and plug into the other, then solve for F.

 

[aero_zeppelin]

shoot... yeah, I just realized my mistake there... loll thanks a lot for the help!