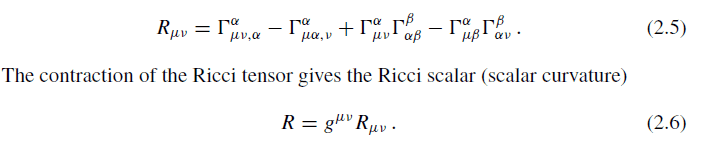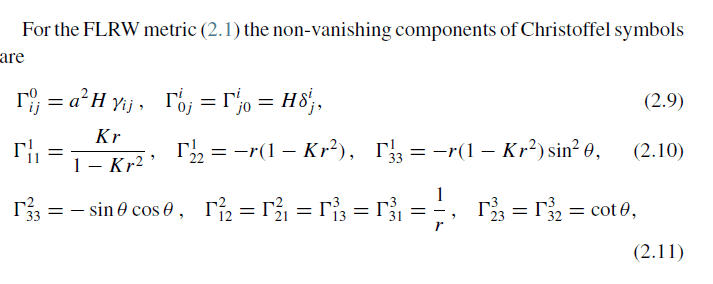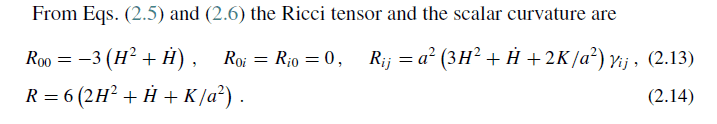SUMMARY
This discussion focuses on the calculations necessary to derive equations (2.13) and (2.14) from equations (2.5), (2.6), (2.9), (2.10), and (2.11) in the context of General Relativity and Dark Energy. Participants emphasize the importance of adhering to homework guidelines, particularly in presenting calculations clearly and legibly. The need for step-by-step explanations is highlighted to facilitate understanding and assistance. The discussion underscores the collaborative nature of problem-solving in physics.
PREREQUISITES
- Understanding of General Relativity principles
- Familiarity with mathematical notation used in physics
- Ability to perform algebraic manipulations and substitutions
- Knowledge of the specific equations referenced (2.5, 2.6, 2.9, 2.10, 2.11)
NEXT STEPS
- Review the derivation of equations in General Relativity
- Study the implications of Dark Energy on cosmological models
- Learn about the significance of homework guidelines in collaborative learning
- Explore step-by-step problem-solving techniques in physics
USEFUL FOR
Students of physics, educators guiding homework assignments, and anyone interested in the mathematical foundations of General Relativity and Dark Energy.