From where did the ##ie\gamma## come into the picture? (QED)

[Wrichik Basu]

While reading the electromagnetic vertex function at one loop, the authors of the book I am reading, wrote down the following vertex function:

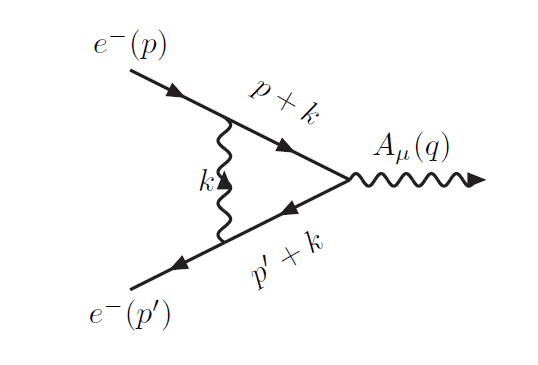
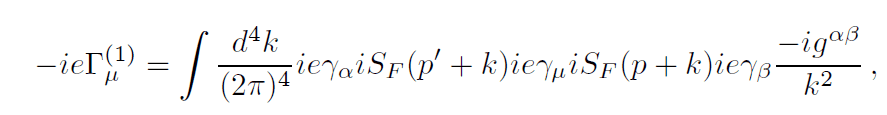corresponding to this Feynman diagram:

The superscript in $\Gamma$ is the number of loops being considered.

My problem is with the equation. I know that they are considering the loop only, leaving out the external Fermion and photon lines. I understand how the two propagators, $iS_F(p' + k)$ and $iS_F(p + k)$ have come, and also how the last term has come (from the propagator of photon field). But why are the $ie\gamma$ present before each propagator term? While writing the Feynman amplitude, we don't add these terms. Why are we adding them here?

N.B.: Sorry for not typing out the equation. It was a long one, and I thought you can understand from the scan itself, so I posted a screenshot. In case of any discrepancy, let me know, and I shall type it out.

 

[haushofer]

And the book you're reading is...?

 

[Wrichik Basu]

And the book you're reading is...?

This specific case is taken from the book An Introductory Course in Particle Physics by Palash B. Pal. I am actually reading the QFT book by the same author, but as I couldn't understand something in the latter, I referred to the former.

It is very much possible that I have missed something, as I am a beginner. Please point out the problems so that I can learn.

 

[HomogenousCow]

They simply come from the QED interaction term. You can try to calculate the three-point function to first order and see that it comes out this way.

 

[Wrichik Basu]

They simply come from the QED interaction term.

I remembered as soon as you said that: they come from the vertices because the Feynman rule for the fermion-photon vertex is $ie\gamma_\mu$. My foolishness.

Just tell me if I have got this correct:

When I am writing the Feynman amplitude from the Feynman diagram, the steps are:

1. Check whether there are internal loops. If there are no loops but just simple internal boson or fermion (or photon) lines, I will proceed normally.
2. If there are loops, I will first write down the "inner" vertex function for all the internal lines. This will include any vertex that occurs in the loop.
3. Then I will proceed to write the full Feynman amplitude (for the whole diagram). This will include external lines and the "inner" vertex function which I have just computed.

This is actually making sense now.

 

[HomogenousCow]

Have you gone through the full derivation at least once by yourself? Because it really helps to see where everything is coming from.

By "full derivation" I mean something like:
1. Expanding the Greens function to some order
2. Evaluating the term(s) either with Wick's theorem or a path integral
3. Feed your results into the LSZ to obtain the scattering amplitude

It's a lengthy exercise but it really helps demystify the Feynman rules.

 

[haushofer]

This specific case is taken from the book An Introductory Course in Particle Physics by Palash B. Pal. I am actually reading the QFT book by the same author, but as I couldn't understand something in the latter, I referred to the former.

It is very much possible that I have missed something, as I am a beginner. Please point out the problems so that I can learn.

To be honest, it has been a while for me. I can see on the right hand side where the three factors of $i e \gamma$ come from, since you have three vertices there. But why the left hand side has only one single factor of $i e$, I can't see. I guess it's in the definition of $\Gamma$, but as I said, it has been a while and I'm probably overlooking something silly.

 

[Wrichik Basu]

Have you gone through the full derivation at least once by yourself? Because it really helps to see where everything is coming from.

By "full derivation" I mean something like:
1. Expanding the Greens function to some order
2. Evaluating the term(s) either with Wick's theorem or a path integral
3. Feed your results into the LSZ to obtain the scattering amplitude

It's a lengthy exercise but it really helps demystify the Feynman rules.

Yes, I did that after posting my previous message in this thread. Things see now clear.