Function if a plane dropping a bomb.

[Metalsie]

Vertically:
The initial velocity: =0
Acceleration: a=-9.8
Target Height: y=0
Current Height: y=8000m
time=40.40

Horizontally:
Velocity=133.88
Acceleration=0
time=40.40

Using these values, I have calculated that the bomb will drop 5408.75 meters away. Now I am trying to find the total distance the bomb travels when its dropping. In order to do that, I need a function for the movement of the missile.

How can I find that function? And by function I mean its representation in terms of y=x

Edit: I used the free fall formula and got

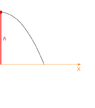
f(x)=-4.9x^2+8000

When I graph this, the curve doesn't even come close to 5000 on the x plane. Is there a way to show it from the perspective of someone on the ground?

 

[MarkFL]

To find the total distance the bomb travels, you can use the arc-length formula:

$$s=\int_a^b\sqrt{\left(\d{x}{t}\right)^2+\left(\d{y}{t}\right)^2}\,dt$$

Can you find the values you need for this formula?

 

[Metalsie]

Yes that's the formula I'm trying to use. sqrt(1+(dx/dy)^2)

I need a function to derive first but I don't know how to get that function. I found ways to calculate the function that is launched from a cannon which goes up and down, a way to calculate the free fall function, but not a function where one is dropped with a horizontal movement.

View attachment 3788

It looks something like this. I need to find the function of this curve.

 

[MarkFL]

We are given:

$$a=0$$

$$b=40.4$$

$$\d{x}{t}=133.88$$

And we can infer:

$$\d{y}{t}=-9.8t$$

So, plug those in...what do you get?