Function of Partition: Understanding Array Partitioning Process

[evinda]

Hello! (Wave)

The following pseudocode is given:

partition(A,p,r){
  x<-A[r]
  i<-p-1
  for j<-p to r-1
       if A[j]<=x then
          i<-i+1
          swap(A[i],A[j])
  swap(A[i+1],A[r])
  return i+1

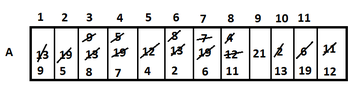
I have to describe the function of [m] partition [/m] at the array: $A= \langle 13, 19, 9, 5, 12, 8, 7, 4, 21, 2, 6, 11 \rangle$.I found the following:
View attachment 4066

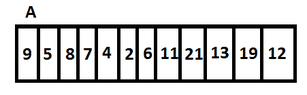
So the final form of the array is:View attachment 4067

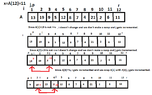
But how could I describe the function of [m] partition [/m] at the array? (Thinking)

 

[evinda]

I have to make a step-by-step trace and write at each step what the algorithm does.So do I have to write at each step the value that [m] i [/m] gets and the swap that is done?

 

[I like Serena]

I have to make a step-by-step trace and write at each step what the algorithm does.

So do I have to write at each step the value that [m] i [/m] gets and the swap that is done?

I suggest writing at each step the value of [m]i[/m], [m]j[/m], and the full contents of [m]A[/m]. (Wasntme)

 

[evinda]

I suggest writing at each step the value of [m]i[/m], [m]j[/m], and the full contents of [m]A[/m]. (Wasntme)

So should I do it in the way as follows? (Thinking)

View attachment 4078

Or should I write it in an other way?

 

[I like Serena]

So should I do it in the way as follows? (Thinking)

Or should I write it in an other way?

Looks good. (Smile)

Do you already have an idea what is happening? (Thinking)

Where do the elements that are smaller than $x$ end up? (Wondering)

 

[evinda]

Looks good. (Smile)

Do you already have an idea what is happening? (Thinking)

Where do the elements that are smaller than $x$ end up? (Wondering)

$x$ ends up at its right position and at its left there will be all the elements that are smaller than $x$ and at its right there will be all the elements that are greater than $x$, right?So after drawing 11 times the array, should I write this conclusion? (Wasntme)

 

[I like Serena]

$x$ ends up at its right position and at its left there will be all the elements that are smaller than $x$ and at its right there will be all the elements that are greater than $x$, right?

Yep.

So after drawing 11 times the array, should I write this conclusion? (Wasntme)

If it were me, I'd skip a couple of steps, since I'd already know what was happening.
And then I'd write down the last 2 steps or so, followed by the conclusion. (Wasntme)

 

[evinda]

Yep.

Nice!

If it were me, I'd skip a couple of steps, since I'd already know what was happening.
And then I'd write down the last 2 steps or so, followed by the conclusion. (Wasntme)

So could I for example write the first three steps and then the last two ones? (Thinking)

 

[I like Serena]

Nice!So could I for example write the first three steps and then the last two ones? (Thinking)

Sounds good. (Smile)

The important part is that all cases are included.
That is a case that a number is less than x and also a case that a number is more than x. (Nerd)

Btw, what would happen if one of the numbers were equal to x? (Wondering)

 

[evinda]

Sounds good. (Smile)

The important part is that all cases are included.
That is a case that a number is less than x and also a case that a number is more than x. (Nerd)

A ok... (Nerd)

Btw, what would happen if one of the numbers were equal to x? (Wondering)

Then [m]i[/m] would be incremented and we would make a swap, right? (Smile)

 

[I like Serena]

hen [m]i[/m] would be incremented and we would make a swap, right? (Smile)

Yes.
I'd say that an element equal to x=A[r] will end up to the left of the position where A[r] will end up at the end. (Nerd)

 

[evinda]

Yes.
I'd say that an element equal to x=A[r] will end up to the left of the position where A[r] will end up at the end. (Nerd)

Nice!
I want to explain why the execution time of [m] partition [/m] at an array of length $n$ is $\Theta(n)$.
Could I say the following? (Thinking)

We assume that assignments, accesses at elements of array, call of swap, additions, comparisons between numbers and return of value require constant time.
The for loop is executed $r-1-p+1=r-p=n-1$ times.
So the time execution is $b+d(n-1)+e \in \Theta(n)$
where $b,d,e$ constants.

 

[I like Serena]

Nice!
I want to explain why the execution time of [m] partition [/m] at an array of length $n$ is $\Theta(n)$.
Could I say the following? (Thinking)

We assume that assignments, accesses at elements of array, call of swap, additions, comparisons between numbers and return of value require constant time.
The for loop is executed $r-1-p+1=r-p=n-1$ times.
So the time execution is $b+d(n-1)+e \in \Theta(n)$
where $b,d,e$ constants.

What if I call [m]partition(A, 1, 1)[/m], where A is an array with n=100000 elements?
Does it take ~100000 operations? (Wondering)

 

[evinda]

What if I call [m]partition(A, 1, 1)[/m], where A is an array with n=100000 elements?
Does it take ~100000 operations? (Wondering)

I am asked to explain why the execution time of [m] partition [/m] at an array of length $n$ is $\Theta(n)$.
So don't we suppose that $r-p+1=n$? Or am I wrong? (Thinking)

 

[I like Serena]

I am asked to explain why the execution time of [m] partition [/m] at an array of length $n$ is $\Theta(n)$.
So don't we suppose that $r-p+1=n$? Or am I wrong? (Thinking)

In an answer I would say: "If we apply the algorithm at a section of an array of length $n=r-p+1$, then...".
Perhaps I'm a bit of a nitpicker, but I prefer to be accurate. (Wasntme)

 

[evinda]

In an answer I would say: "If we apply the algorithm at a section of an array of length $n=r-p+1$, then...".
Perhaps I'm a bit of a nitpicker, but I prefer to be accurate. (Wasntme)

I prefer it too... (Nod) Thanks a lot! (Smile)