Function Pop for a static stack

[evinda]

Hello! (Smile)

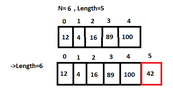
A static stack is implemented with the use of a one-dimensional array $A$.
Suppose that we have a pointer $S$ to a struct that has two fields, the array $A$ and the integer Length, and represents a stack.

According to my notes, the operation [m] Push [/m] for a static stack is the following:

void Push(Pointer S, Type x)
  if (S->Length==N) then error;
  else {
         S->Length=S->Length+1;
         (S->A)[S->Length-1]=x;
}

But don't we have to check also if [m]S->Length+1==N[/m] ? Or am I wrong?

 

[I like Serena]

Hey! (Wave)

What is the reason that we would have to check [m]S->Length+1==N[/m] ? (Wondering)

The first check is to see if the stack is full. If it isn't, we can add the new element.

 

[evinda]

Hey! (Wave)

What is the reason that we would have to check [m]S->Length+1==N[/m] ? (Wondering)

The first check is to see if the stack is full. If it isn't, we can add the new element.

I thought so because we check if the stack is full for a given [m] Length [/m] and then we increment the [m] Length [/m] and after that we put a new element.

So it will be for example like that:

View attachment 3865

Right? So we check if [m] Length==N [/m] because that will be the position at which we will place the new element, right? (Thinking)

 

[I like Serena]

I believe the new element is effectively placed at N-1. (Thinking)

When yet another element is pushed, we find that Length == N, and no other element will fit. (Wasntme)

 

[evinda]

I believe the new element is effectively placed at N-1. (Thinking)

Will the new element not be placed at the postion [m]S->length[/m] before we change it? Or am I wrong? (Worried)

 

[I like Serena]

Will the new element not be placed at the postion [m]S->length[/m] before we change it? Or am I wrong? (Worried)

Let's take a close look at your example. (Thinking)

Initially we have N=6 and S->Length=5.

Statement	Assertion
[m]if (S->Length==N) then error;[/m]	No error
[m]else {[/m]	S->Length == N -1
[m]S->Length=S->Length+1;[/m]​	S->Length == N
[m](S->A)[S->Length-1]=x;[/m]​	S->A[N-1] == x
[m]}[/m]

In other words: the new element is placed at index N - 1, which is indeed 5. (Wasntme)

 

[evinda]

Let's take a close look at your example. (Thinking)

Initially we have N=6 and S->Length=5.

Statement	Assertion
[m]if (S->Length==N) then error;[/m]	No error
[m]else {[/m]	S->Length == N -1
[m]S->Length=S->Length+1;[/m]​	S->Length == N
[m](S->A)[S->Length-1]=x;[/m]​	S->A[N-1] == x
[m]}[/m]

In other words: the new element is placed at index N - 1, which is indeed 5. (Wasntme)

I see... (Nod) But this happens only when at the beginning it holds that [m] S->Length=N-1[/m]. In the general case, we put the new element at the position [m] S->Length [/m] before incrementing it, right?

 

[I like Serena]

I see... (Nod) But this happens only when at the beginning it holds that [m] S->Length=N-1[/m]. In the general case, we put the new element at the position [m] S->Length [/m] before incrementing it, right?

Let's redo that for the more general case, with the initial assumption that S->Length <= N. (Thinking)

Statement	Assertion
	S->Length <= N
[m]if (S->Length==N) then[/m]
[m]error;[/m]​	S->Length == N and ERROR
[m]else {[/m]	S->Length < N
[m]S->Length=S->Length+1;[/m]​	S->Length <= N
[m](S->A)[S->Length-1]=x;[/m]​	S->A == x where i <= N - 1

[tr]
[td][m]}[/m][/td]
[td]S->Length <= N[/td]
[/tr]

In other words, if the stack was initially empty, any element will placed at an index <= N - 1.
And S->Length will always be <= N. (Mmm)