yilmaz
- 8
- 0
- Homework Statement
- this is actually not a homework
- Relevant Equations
- tsin(ct)
Hi;
This is in fact not a homework question, but it rather comes out of personal curiosity.
If you look at the graph of the two functions in the image attached, what is the simplest functional representation for such a symmetrical pattern?
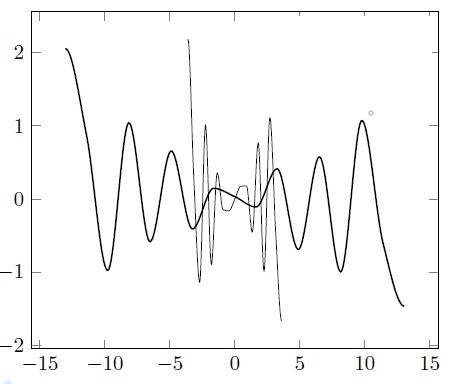
This is in fact not a homework question, but it rather comes out of personal curiosity.
If you look at the graph of the two functions in the image attached, what is the simplest functional representation for such a symmetrical pattern?