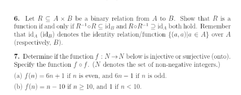Functions and Relations: Proving R is a Function from A to B

[Sharon]

Let R\subseteq A*B be a binary relation from A to B , show that R is a function if and only if R^-1(not) R \subseteq idB and Rnot aR^-1 \supseteq both hold. Remember that Ida(idB) denotes the identity relation/ Function {(a.a)|a€ A} over A ( respectively ,B)
Please see the attachment ,I couldn't write the question properly, and this is only one question but I need help with another one too.

 

[Evgeny.Makarov]

$\text{id}_A\subseteq R\circ R^{-1}$ means that for every $a\in A$ we have $(a,a)\in R\circ R^{-1}$. By the definition of composition of relation, there exists a $b\in B$ such that $(a,b)\in R$ and $(b,a)\in R^{-1}$. In fact, $(a,b)\in R$ implies $(b,a)\in R^{-1}$, so $(b,a)\in R^{-1}$ does not add useful information, but we have shown that for every $a\in A$ there exists a $b\in B$ such that $(a,b)\in R$.

Suppose now that $(a,b)\in R$ and $(a,b')\in R$ for some $a\in A$ and $b,b'\in B$. Then $(b,a)\in R^{-1}$, so $(b,b')\in R^{-1}\circ R$. But since $R^{-1}\circ R\subseteq\text{id}_B$, it follows that $b=b'$.

It is left to prove the other direction, where the fact that $R$ is a function implies the two inclusions.

Concerning problem 7, could you write what you have done and what is not clear to you? Also, please read the https://mathhelpboards.com/rules/, especially rule #11 for the future.