LCSphysicist
- 644
- 162
- Homework Statement
- A violin string on a violin is of length L and can be considered to be
fastened at both ends. The fundamental of the open string has a frequency
fo. The violinist bows the string at a distance L/4 from one end and touches
the string lightly at the midpoint.
"Under this condition, what is the lowest frequency he can excite?"
- Relevant Equations
- All below
Why is this wrong?:
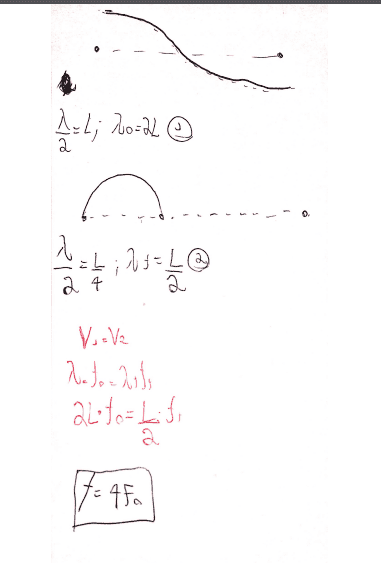
That is, why is not f = 4fo?
Oh. And my figure 1 can be wrong, because maybe i got confused if the string was open or closed in the boundaries, anyway this change nothing the relations (1)
That is, why is not f = 4fo?
Oh. And my figure 1 can be wrong, because maybe i got confused if the string was open or closed in the boundaries, anyway this change nothing the relations (1)