Galileo and the centripetal force experienced by objects on the rotating earth

[A_B]

Hi,

This question is about a discussion in the two chief world systems, the second day about p 230 in the modern science library edition (around figures 10 and 11). I haven't found the excerpt online so I hope someone has the book.

As an objection to a rotating earth, the claim that any object on its surface must experience a centripetal acceleration and thus be projected from the surface of the Earth is considered.

Galileo argues that the downward motion of anybody is always sufficient to overcome its tendency to to be projected from the rotating sphere.

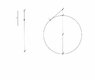
I don't understand the argument at all, for example in his discussions relating to figure 11 he seems to be comparing distances (the arc) with velocities (the perpendiculars).

Furthermore, Nowhere in the argument is there used anything such that it could not be applied to a rotating wheel with objects loosely attached to its circumference. Galileo knows full well that by spinning the wheel fast enough, the loosely attached objects would break free, but to me it seems that the argument would exclude this possibility as well.



(PS I am aware of the Newtonian description for this problem. It can be easily derives from the radius and period of revolution of the Earth that the centripetal acceleration of any object is about 0.036ms-2 and its acceleration due to gravity is about 10ms-2, so that objects stay on the surface of the earth. The question is more about understanding Galileo's line of though then about understanding the phenomenon)


Thanks,

A_B

 

[mfb]

Galileo argues that the downward motion of anybody is always sufficient to overcome its tendency to to be projected from the rotating sphere.

This is true in special cases only (slow rotation, large mass, ...). On the other hand, every object which rotates too quick ejects mass in an orbit (or even in outer space), and slows down by this, until it is stable. In that way, every real object satisfies Galileo's assumption.

I don't have the book, so I can't check the figures.

 

[zoobyshoe]

The whole book is online here. I looked all over for the argument you mention but couldn't find it.

http://archimedes.mpiwg-berlin.mpg.de/cgi-bin/toc/toc.cgi?step=thumb&dir=galil_syste_065_en_1661

 

[A_B]

Thanks you, Mfb and Zoobyshoe, for you replies,

In the version linked to by you, Zoobyshoe, the discussion start at about plate 179 and runs through to plate 189. Unfortunately the diagrams are missing (they should be found at the end of the second day's dialogue, but the links are dead, so I reconstructed them, as they may be difficult to construct based on the description in the text alone.

 

[zoobyshoe]

As an objection to a rotating earth, the claim that any object on its surface must experience a centripetal acceleration and thus be projected from the surface of the Earth is considered.

What would project the body is the 'impetus' given to it by the rotating earth. Simplicio thinks that if the Earth were rotating, everything on the surface would be thrown off. Salvatio's argument is that the centripetal acceleration (i.e. gravity) is what prevents this.

Galileo argues that the downward motion of anybody is always sufficient to overcome its tendency to to be projected from the rotating sphere.

The "downward motion" is an acceleration, not just uniform motion in a right line. The motion the projectile would have along the tangent to the Earth would be mere motion in a right line. He gets Simplicio to understand that whatever motion the body has in the direction the Earth is rotating has no force behind it. Its motion is inertial. The force of gravity, however, is constant and causes a constant centripetal acceleration (acceleration toward the center of the earth).

Regardless, Simplicio has a breakdown and says he still thinks lighter objects should be projected off the Earth if the Earth were actually rotating.

I don't understand the argument at all, for example in his discussions relating to figure 11 he seems to be comparing distances (the arc) with velocities (the perpendiculars).

In figure 11 he's explaining why a lighter and lighter object does not have a greater and greater propensity to be thrown off the Earth on a tangent, as Simplicius thinks it should. I have to confess that in two readthroughs, I haven't fathomed this explanation yet. The vertical lines represent the velocities an object would have after having fallen for the amount of time indicated on the horizontal line at the top. The longer the vertical line the greater the velocity due to the fact more time has passed and the object is being accelerated. I got lost when he started considering things diminishing to infinite smallness as you approach point A. The arc somehow represents a change in the rate that diminishment would occur considering objects of smaller and smaller weight (I think but am not sure).

I read his other book, Two New Sciences (or most of it) and found it very slow going. The language is very difficult. I had to stop and consider each sentence a very long time in a lot of cases. I might just get Two Chief World Systems out of the library so I can ponder fig. 11 with the text at hand when I'm out having coffee.

 

[zoobyshoe]

Galileo argues that the downward motion of anybody is always sufficient to overcome its tendency to to be projected from the rotating sphere.

I don't understand the argument at all...

I went to the library and got a much clearer translation than the online one.

When Salviati says: "So there is no danger, however fast the whirling and however slow the downward motion, that the feather (or even something lighter) will begin to rise up. For the tendency downward always exceeds the speed of projection," he has just verbally laid out the geometrical proof that Simplicio's conditions for projection are wrong. He hasn't proven that an object can't be projected from the earth, just that, under the conditions set by Simplicio, "the tendency downward always exceeds the speed of projection".


Salviati is specifically responding to Simplicio's belief that the object must be projected in any case where it's velocity along the tangent exceeds its velocity along the secant, downward.

"Salv. To have projection occur, it is required that the impetus along the tangent prevail over the tendency along the secant. Is that not so?

Simp. It seems so to me."

The point of figure 10 is to prove, geometrically, that the situation Simplicio describes, tangent speed exceeding secant speed, actually always exists during any rotation and yet, if there is also any centripetal tendency, objects are not projected. Therefore, there must be something wrong with Simplicio's assumption that this is what is required for projection.

Salviati has prompted Simplicio to specifically state a ratio of tangential speed to downward speed that would guarantee projection. Simplicio, to be on the safe side, throws out the ratio of a million to one:

"Salv. ...Say then, how much faster you think the latter motion should be made in order to suffice.

Simp. I shall say that if, for example, the latter were a million times faster than the former, the feather (and the stone likewise) would be extruded."

Salviati doesn't care because he knows his geometry and knows that, whatever ratio Simplicio throws out, he can find it in his geometric figure (ad infinitum) and, to the extent that figure represents any rotating wheel where the strings holding the objects to the circumference do not break, he can say, 'That ratio you fear always exists here, at such and such a point along the tangent, yet we see no projection, do we?'

Galileo hasn't constructed an argument against a wheel being able to rotate fast enough for the strings to break. He has simply demonstrated that the breaking point can't be considered dependent on the ratio of tangential speed to centripetal speed, at least not in the way Simplicio thinks it would be (that is: in the absence of consideration of the strength of the string).

I think what's going on here is that Galileo is addressing what must have been a then common Aristotelian criticism of the notion that the Earth was revolving. The Aristotelians must have said, "It's obvious that for projection a tangential speed must simply exceed a centripetal speed. Since the Earth is so large, the speed that a point on the surface would have in rotating once a day must, obviously, be many times in excess of its downward speed, and this would assure projection of anything on the surface of the Earth into space. Therefore, the Earth cannot be rotating."

Galileo's answer is that an excess of tangential speed to centripetal is geometrically guaranteed in all cases of rotation, yet we do not see all slingshots, and other weights swung around, automatically and instantly breaking apart. Therefore there is something wrong with the assumption that 'tangential speed in excess of speed along the secant = projection', and he castigates Simplicio for not already realizing this is the case ("...deficiency...in geometry.").

No one asks Salviati about the wheel rotated fast enough that the strings actually do break, but since you asked I think the answer is that gravity never ever, ever breaks the way a string does. As long as an object is in a gravitational field, that field gives it a centripetal acceleration of some number of ms/s in complete disregard of how fast it is moving along any other vector. The horizontal muzzle velocity of a bullet, for example, has no effect whatever on how fast it drops to the earth. When a string breaks the centripetal acceleration stops instantly. But, you can never go fast enough to "break" gravity and fly off on a straight tangent. I think there's a good chance that's the concept Galileo was waving his hand at when Salviati says, "the tendency downward always exceeds the speed of projection".

I hope that helps. I haven't looked at fig.11 again yet. It took me two or three hours of pondering fig. 10 to grasp what it was supposed to prove and how it proved it. Had to do some googling till I traced it back to Euclid.

http://www.proofwiki.org/wiki/Tangent_Secant_Theorem

This is another reason Galileo is hard to read: he assumes, or at least desires, a facile knowledge of Euclid and Archimedes on the part of his reader. (Notice how Salviati criticizes Simplicio when he doesn't automatically recall geometric theorems off the top of his head.)