Guillem_dlc
- 188
- 17
- Homework Statement
- We have an Q=2nC-load uniformly distributed on a solid dielectric sphere of R=1m-radius with center at the coordinate origin of an Oxyz axis system. At the O centre of this sphere there is a negative point charge q=−1nC. Let us consider the points of space P=(0.3,0.4,0)m and S=(1,2,2)m. Calculate:
(a) The electric field vector at points P and Q.
(b) The difference in potential between these points, i.e. V(S)−V(P).
- Relevant Equations
- Gauss-Law
The load system formed by the point load and the load distribution generates two regions in space corresponding to r<1m and r>1m, i.e. inside and outside the sphere. Given the symmetry of the distribution, by means of the Gaussian theorem we can find the modulus of the field at a distance r from the center.
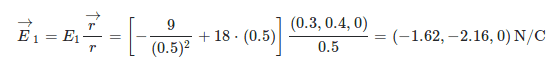
Until the last equation I have it well but the result gives me different. The first component is: [−36+9]⋅(0.3)/(0.5) isn't it? Or I don't see it ...
- Region r<1m:
Until the last equation I have it well but the result gives me different. The first component is: [−36+9]⋅(0.3)/(0.5) isn't it? Or I don't see it ...