shawn87411
- 17
- 0
This isn't a specific problem, I just can't remember how to solve problems like these.
I attached a brief picture.
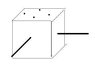
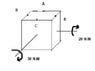
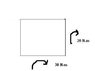
The dots on the top are screws that hold the box in place. There's torques on both the shafts in the clockwise direction (shaft coming out towards you is 30 and the one going horizontal is 20) and I know the distance between the screws. there's only vertical forces on the screws. I just can't remember how to go about solving it - I know I do the summation of torques is 0 but I forgot how it works in a 3D plane.
I'm guessing you do the sum of the torques in the direction of one of the torques is 0 and then do the same for the other direction which gives 2 equilibrium equations. I'm missing where the other 2 come from?
I attached a brief picture.
The dots on the top are screws that hold the box in place. There's torques on both the shafts in the clockwise direction (shaft coming out towards you is 30 and the one going horizontal is 20) and I know the distance between the screws. there's only vertical forces on the screws. I just can't remember how to go about solving it - I know I do the summation of torques is 0 but I forgot how it works in a 3D plane.
I'm guessing you do the sum of the torques in the direction of one of the torques is 0 and then do the same for the other direction which gives 2 equilibrium equations. I'm missing where the other 2 come from?
Attachments
Last edited: