SUMMARY
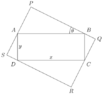
The discussion focuses on determining the possible values of the area \( A \) of a rectangle circumscribing another rectangle with sides \( x \) and \( y \). The area \( A^2 \) is expressed as \( A^2 = (x\cos\theta + y\sin\theta)(x\sin\theta + y\cos\theta) \), leading to the conclusion that \( A \) ranges from \( \sqrt{xy} \) to \( \frac{1}{\sqrt{2}}(x+y) \) as \( \theta \) varies between \( 0 \) and \( \frac{\pi}{2} \). The minimum area occurs at \( \theta = 0 \) or \( \frac{\pi}{2} \), while the maximum area occurs at \( \theta = \frac{\pi}{4} \).
PREREQUISITES
- Understanding of basic geometry concepts, particularly rectangles
- Familiarity with trigonometric functions such as sine and cosine
- Knowledge of the properties of angles and their ranges
- Ability to manipulate algebraic expressions involving squares and products
NEXT STEPS
- Explore the derivation of area formulas for circumscribed shapes
- Study the implications of trigonometric identities in geometry
- Investigate optimization techniques in geometric contexts
- Learn about the applications of these concepts in real-world scenarios, such as architecture and design
USEFUL FOR
Mathematicians, geometry enthusiasts, educators, and students looking to deepen their understanding of geometric relationships and trigonometric applications.