Discussion Overview
The discussion revolves around finding the radius of a circle inscribed in a triangle, with participants exploring various methods and reasoning related to geometric properties and relationships within the triangle.
Discussion Character
- Exploratory
- Mathematical reasoning
- Debate/contested
Main Points Raised
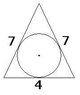
- One participant presents a proposed answer for the radius as \(\frac{2\sqrt{5}}{3}\) but seeks an explanation for this result.
- Another participant suggests a method involving drawing perpendicular bisectors from the triangle's edges to the center of the inscribed circle, indicating that the radius can be derived from the areas of the smaller triangles formed.
- A different approach is introduced, where a participant claims that the radius perpendicular to the base bisects the base, leading to a relationship involving the lengths of the sides and the Pythagorean theorem.
- Another solution is proposed using two congruent triangles, establishing a ratio involving the segments created by the radius and the triangle's dimensions.
- One participant questions how certain values for the segments created by the radius tangent to the longer side are determined, specifically referencing segments of lengths 5 and 2.
- A repeated question seeks clarification on the reasoning behind the segment lengths, suggesting that the smallest segment is half of the triangle's base.
Areas of Agreement / Disagreement
Participants present multiple competing methods and reasoning for finding the radius, indicating that there is no consensus on a single approach or solution. The discussion remains unresolved with various interpretations and calculations being explored.
Contextual Notes
Some methods rely on specific geometric properties and relationships that may not be universally accepted or understood, leading to potential gaps in assumptions or definitions. The discussion includes various mathematical steps that are not fully resolved.