Discussion Overview
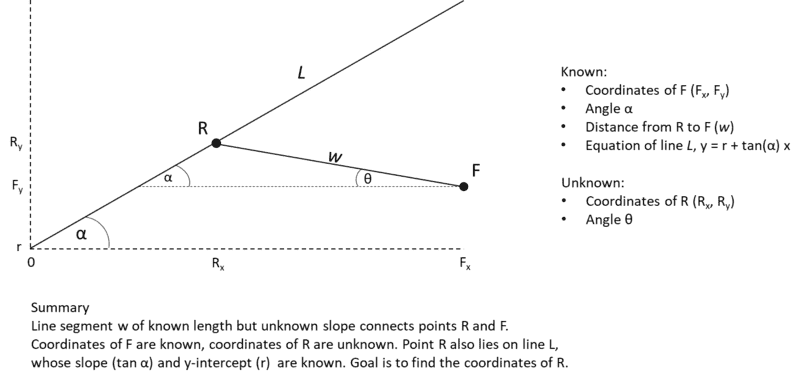
The discussion revolves around a geometry/trigonometry problem involving a point in 2-D space and a line segment of known length connecting this point to another point on a defined line. Participants explore the mathematical relationships and constraints involved in determining the unknown coordinates of the second point.
Discussion Character
- Exploratory
- Technical explanation
- Mathematical reasoning
- Debate/contested
Main Points Raised
- One participant describes the problem setup, noting the known point (F), the unknown point (R) on a line (L) with a known slope and y-intercept, and expresses confidence that the problem should be solvable.
- Another participant asks for clarification on the original poster's (OP) attempts and whether the problem is for schoolwork or a personal project.
- Several participants discuss the equations involved, including the line equation and the circle equation representing the segment's length, and note that the intersection of these equations leads to two potential solutions for point R.
- One participant mentions the complexity of the resulting equations and the challenges faced when attempting to simplify them for coding purposes.
- Another participant suggests using known values to substitute into the equations to simplify the problem further.
- Some participants share external resources for understanding the intersection of lines and circles, indicating various methods to approach the problem.
- There is a discussion about the potential for using right triangles to find parameters related to the problem, though one participant expresses skepticism about the simplicity of this approach given the diagram.
Areas of Agreement / Disagreement
Participants generally agree on the mathematical framework of the problem but express differing opinions on the best approach to solve it. There is no consensus on a single method or solution, and the discussion remains unresolved.
Contextual Notes
Participants note the complexity of the equations involved and the potential for multiple solutions, as well as the challenges in simplifying the expressions for practical implementation in coding.
Who May Find This Useful
This discussion may be useful for individuals interested in geometry, trigonometry, and mathematical problem-solving, particularly in contexts involving intersections of geometric shapes and coding applications.