Granddaughter's Math Homework: Understanding an Equation

[yungman]

Summary:: Tripped by my grand daughter's math homework again!

This is the homework of my grand daughter, I don't understand the question:

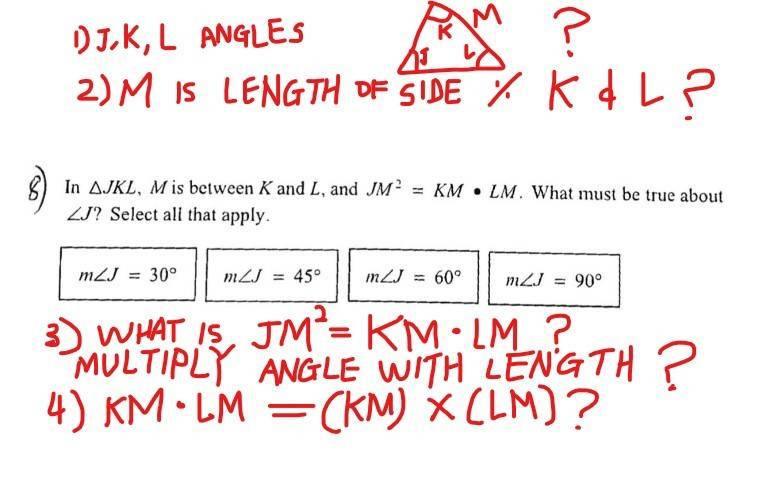
I wrote the questions in red. I have not done geometry for a long time! I don't understand the equation JM^2 = KM . LM. Is the "dot" just multiply? or is it a dot product like in vector? Please explain. I can't even start to solve the problem until I understand the question. I never seen anything like this.

Thanks

[Moderator's note: moved from a technical forum.]

 

[jedishrfu]

I think M is any point on the line connecting K and L. Using M, we can construct another line segment JM that connects J and M.

so the line segment JM has a length of JM and the KM and LM line segments have lengths of KM and LM respectively.

The question wants you answer what angle must J be such that:

JM * JM = KM * LM for any point M on the KL line segment

where the asterisk is simply real number multiplication and JM, KM, and LM are length measures.

 

[yungman]

I think M is any point on the line connecting K and L. Using M, we can construct another line segment JM that connects J and M.

so the line segment JM has a length of JM and the KM and LM line segments have lengths of KM and LM respectively.

The question wants you answer what angle must J be such that:

JM * JM = KM * LM for any point M on the KL line segment

where the asterisk is simply real number multiplication and JM, KM, and LM are length measures.

Thanks

This makes it a lot easier. Only one thing is it really does not specify M is the mid point. But it won't work if it doesn't.

This is my work, let me know whether I am right. It's not hard after I understand the question.

I don't get use to angle J or angle K. I am more used to angle KJL and angle JKL. That would be a lot clearer.

If M is not the mid point, it's going to be harder to find.

Thanks

 

[yungman]

Seems like if M is not the mid point, you can make the equation work with any angle less than 180deg. I don't know how to proof it, but there should be some length of the sides of the triangle to make the equation fit. So all the answers are correct in the problem. But I don't know how to proof it.

I tried to use cosine law, but there's too many variables. Anyone know of a way to proof this if M is not a mid point?

Thanks

 

[Delta2]

If the question means that for any point M between K and L it holds $JM^2=KM\cdot LM$ then you have solve it because since it holds for any point, it holds for the mid point as well and from that you proved that J is 90. So J is 90 the only correct answer.

However I am not sure that the question means that. I think it means that there exists a point M (not necessarily the mid point ) such that $JM^2=KM\cdot LM$. Then it is totally different. Then 90 degrees is one possible answers but there might others as well and your answer is incomplete.

BTW in the last line of your work you meant to write that $KJL=\beta+\gamma$ right?

 

[aheight]

Seems like if M is not the mid point, you can make the equation work with any angle less than 180deg. I don't know how to proof it, but there should be some length of the sides of the triangle to make the equation fit. So all the answers are correct in the problem. But I don't know how to proof it.

I tried to use cosine law, but there's too many variables. Anyone know of a way to proof this if M is not a mid point?

Thanks

If it were my test question, I'd check all of them as I agree the angle can be any from 0 to 180 if the point M is anywhere along the segment KL. If you have access to Mathematica, perhaps you can study the code below with KL=1 and as the parameters "t" (angle of MJ on the circle -- the red line) and "a" (length of MJ) are varied we always have red^2=(green)(blue) and since we can scale it for any length KL then we can adjust the triangle with the angle at J to be 0 to 180. Then perhaps formulate it into a proof.

Manipulate[
 p1 = {a Cos[t], a Sin[t]};
 p1G = Graphics@{PointSize[0.01], Point@p1};
 c1 = Graphics@Circle[{0, 0}, a];
 line1 = Graphics@{Red, Line@{{0, 0}, p1}};
 theX = x /. NSolve[x^2 - x + a^2 == 0, x];
 pb1 = Graphics@{PointSize[0.01], Red, Point@{-theX[[1]], 0}};
 pb2 = Graphics@{PointSize[0.01], Blue, Point@{1 - theX[[1]], 0}};
 lineA = Graphics@Line[{{-theX[[1]], 0}, {a Cos[t], a Sin[t]}}];
 lineB = Graphics@Line[{{a Cos[t], a Sin[t]}, {1 - theX[[1]], 0}}];
 lineC = Graphics@{Darker@Green, Line[{{-theX[[1]], 0}, {0, 0}}]};
 lineD = Graphics@{Blue, Line[{{1 - theX[[1]], 0}, {0, 0}}]};
 
 Show[{c1, line1, c1, p1G, pb1, pb2, lineA, lineB, lineC, lineD},
  PlotRange -> 1], {{t, Pi/6}, 0, Pi}, {{a, 1/4}, 1/6, .49}]

 

[Office_Shredder]

It's obviously referring to a triangle that has other properties specified in previous questions, lay off the poor teacher here.

 

[aheight]

I feel I did not adequately explain (label) my plot above and can no longer edit it. Here it is with labels. As "t" is adjusted, the point J move around the circle and as "a" increases, the circle grows larger up to JM=0.49 as the points K and L are adjusted so that at all times $(\overline{JM})^2=(\overline{KM})(\overline{ML})$.

Manipulate[
p1 = {a Cos[t], a Sin[t]};
p1G = Graphics@{PointSize[0.01], Point@p1};
c1 = Graphics@Circle[{0, 0}, a];
line1 = Graphics@{Red, Thickness[0.008], Line@{{0, 0}, p1}};
theX = x /. NSolve[x^2 - x + a^2 == 0, x];
pb1 = Graphics@{PointSize[0.01], Red, Point@{-theX[[1]], 0}};
pb2 = Graphics@{PointSize[0.01], Blue, Point@{1 - theX[[1]], 0}};
lineA = Graphics@Line[{{-theX[[1]], 0}, {a Cos[t], a Sin[t]}}];
lineB = Graphics@Line[{{a Cos[t], a Sin[t]}, {1 - theX[[1]], 0}}];
lineC = Graphics@{Darker@Green, Thickness[0.008],
    Line[{{-theX[[1]], 0}, {0, 0}}]};
lineD = Graphics@{Blue, Thickness[0.008],
    Line[{{1 - theX[[1]], 0}, {0, 0}}]};
t1 = Text["M", {0.05, -0.05}, {0, 0}];
t2 = Text["K", {-theX[[1]], -0.05}];
t3 = Text["L", {1 - theX[[1]], -0.05}];
t4 = Text["J", {a Cos[t], a Sin[t] + 0.05}];

Show[{c1, line1, c1, p1G, pb1, pb2, lineA, lineB, lineC, lineD,
   Graphics@{t1, t2, t3, t4}}, PlotRange -> 1,
  Axes -> True], {{t, 2.08}, 0, Pi}, {{a, 0.47}, 1/6, .49}]

 

[Steve4Physics]

Well, I’m going to add my two pennies worth…

The question is incomplete. It is easy to construct a counter-example to demonstrate that - unless M is the midpoint - m∠J can have a wide range of values. This means m∠J can not be limited to one of the values in the given list.

Counter example:
Point K is at (0,0). Point L is at (10,0). Point M is (say) at (1, 0).
This gives KM = 1 and LM = 9 so that KMhttps://en.ero-video.net/movie/?mcd=5WPwC3W0xNphu39ILM = 1https://en.ero-video.net/movie/?mcd=5WPwC3W0xNphu39I9 = 9.
JM² = KMhttps://en.ero-video.net/movie/?mcd=5WPwC3W0xNphu39ILM = 1https://en.ero-video.net/movie/?mcd=5WPwC3W0xNphu39I9 = 9 which gives JM = 3.
Point J can therefore be anywhere on a circle centred on M and radius 3. A range of values for m∠J is therefore possible.

However if M is the midpoint of KL, then let r = KM = LM.
JM² = KMhttps://en.ero-video.net/movie/?mcd=5WPwC3W0xNphu39ILM = r² which gives JM = r.
This mean KL is the diameter of a circle centred on M and radius r, and J lies on this circle. ∠J is the angle subtended by a diameter and is therefore 90º (Thales’ theorem):
https://www.cut-the-knot.org/Outline/Geometry/AngleOnDiameter.jpg

So it seems most likely that the question neglected to state that M is the midpoint of KL.

 

[kuruman]

Could it be that a key piece of information was omitted from the original diagram, namely that $\overline{JM}$ is perpendicular to $\overline{KL}$? Just asking.

 

[neilparker62]

Could it be that a key piece of information was omitted from the original diagram, namely that $\overline{JM}$ is perpendicular to $\overline{KL}$? Just asking.

Without a doubt! Then $m\angle J=90^{\circ}$ would work.