Graphs of s, v and a for a mass with a piece of paper attached

[AN630078]

Homework Statement

Hello, I am really struggling to sketch the following graphs to show how a mass with a piece of paper attached to it varies with time, over a time period of 2T, for: 1. Energy 2. Displacement 3. Velocity 4. Acceleration

Relevant Equations

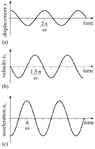
x=Acosωt v=-ωAsinωt a=-ω^2Acosωt

I understand that velocity is defined as the rate of change of position or the rate of displacement; and that acceleration is defined as the rate of change of velocity (it is the derivative of velocity).
Morever, I believe I know that for SHM these graphs vary sinusoidally (I have attached a picture of how I think these should appear).
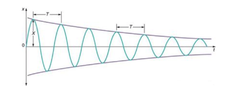
However, for a mass with a piece of paper attached could these graphs be represented by a harmonic oscillator with a small amount of damping? I really do not know where to begin in drawing these, I am very confused.

 

[PeroK]

It's not clear what is the significance of the piece of paper! Is this a translation?

 

[AN630078]

It's not clear what is the significance of the piece of paper! Is this a translation?

I have no idea, I really am very confused. The question just states " Sketch the following graphs to show how a mass with a piece of paper attached to it varies with time, over a time period of 2T"

 

[robphy]

So, the net force is no longer a constant...
you need to model the new net force... a constant plus a new contribution.

If it were damped, what would a sketch of the position-vs-time graph look like?
From that get the other two
[velocity-vs-time is a graph of the slopes of the position-vs-time graph,
acceleration-vs-time is a graph of the slopes of the velocity-vs-time graph
https://phet.colorado.edu/en/simulation/legacy/calculus-grapher [uses Flash]
Not quite as arbitrary as above (but more constructive]:
https://www.geogebra.org/m/dzxdbzAR
https://www.geogebra.org/m/ezKv36tC
]
Or one could work from the acceleration-vs-time [since you know the net force], then get the other two.

Possibly helpful.
https://www.wired.com/2017/04/lets-study-air-resistance-coffee-filters/

 

[AN630078]

So, the net force is no longer a constant...
you need to model the new net force... a constant plus a new contribution.

If it were damped, what would a sketch of the position-vs-time graph look like?
From that get the other two
[velocity-vs-time is a graph of the slopes of the position-vs-time graph,
acceleration-vs-time is a graph of the slopes of the velocity-vs-time graph
https://phet.colorado.edu/en/simulation/legacy/calculus-grapher [uses Flash]
Not quite as arbitrary as above (but more constructive]:
https://www.geogebra.org/m/dzxdbzAR
https://www.geogebra.org/m/ezKv36tC
]
Or one could work from the acceleration-vs-time [since you know the net force], then get the other two.

Possibly helpful.
https://www.wired.com/2017/04/lets-study-air-resistance-coffee-filters/

Thank you for your reply. I have attached what I think the displacement tie graph for a draped oscillator would look like. However, I am uncertain how to find the v-t and a-t graphs from this? Would this be correct anyhow for the s-t graph?

 

[AN630078]

And would the energy-time graph for a damped oscillator be as shown in the attachment ?