Grating Equation & Light Beam: d sin θ = mλ

[nophun6]

Q: The grating equation tells you at what angles different colors of light will appear: d sin θ = mλ
where d is the separation between the lines on the grating,
m is an integer (i.e., m = 0, ±1, ±2, ±3, etc.) known as the diffraction order number,
λ is the wavelength (with the same length units as d), and
θ is the angle at which light with wavelength λ is diffracted.

Make a sketch based on the figure below to show a narrow parallel beam of white light shining onto a grating with line separation d = 1150 nm. Show the angles for red and blue light for m = 0, +1, and –1 by drawing them in appropriate colors

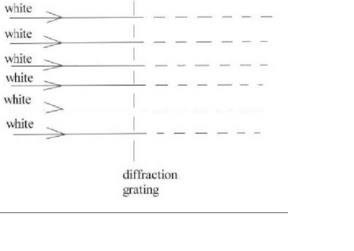
I am confused on how to start this problem. Suggestions on starting points are appreciated.
Thanks.

 

[andrevdh]

Since the wavelengths for the two colours are not given you should choose your own, maybe use \lambda_{red}=700\ nm,\ \lambda_{blue}=\ 500\ nm, and then work the diffraction angles out for the various orders for each of the two colours. It seems this is more a qualitative than quantitative question in spite of the given grating spacing.

 

[tyco05]

It does seem more like a qualitative question... however, you are given enough information to solve for the diffraction angles.

You know:

d*sin(theta) = m*lambda

You are given (if you choose your blue and red wavelengths as Andre suggested) all variables except theta.

It's a matter of transposing the equation so that you have:

theta = something (it's up to you to work this out)

and then applying it three times for each wavelength (m= 0 , +1 and -1)

With this information, you can draw an accurate sketch, you should have 3 blue lines and three red lines...