TopsyKrate
- 1
- 1
- Homework Statement
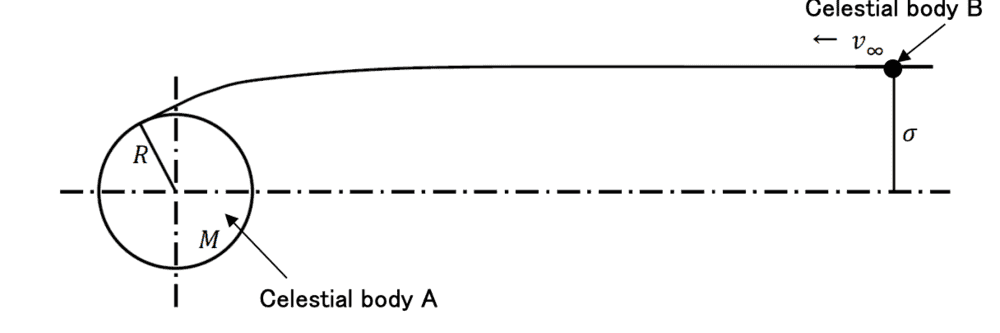
- There is a spherical celestial body A with the radius of 𝑅 and the mass of 𝑀. As
shown in figure, consider movement of a celestial body B of which relative
velocity at infinity is 𝑣∞ with respect to the celestial body A and the mass is
negligible compared to the celestial body A. At infinity, the celestial body B moves
in the horizontal direction shown in the Figure, and the distance from the straight
line which passes through the center of the celestial body A and is parallel to the
movement direction of the celestial body B
Express the condition of 𝜎 where the celestial body B collides against the
celestial body A
- Relevant Equations
- GM/R
Express the condition of 𝜎 where the celestial body B collides against the
celestial body ASo this is the original figure of the problem.
 This is my attempt at a solution
This is my attempt at a solution
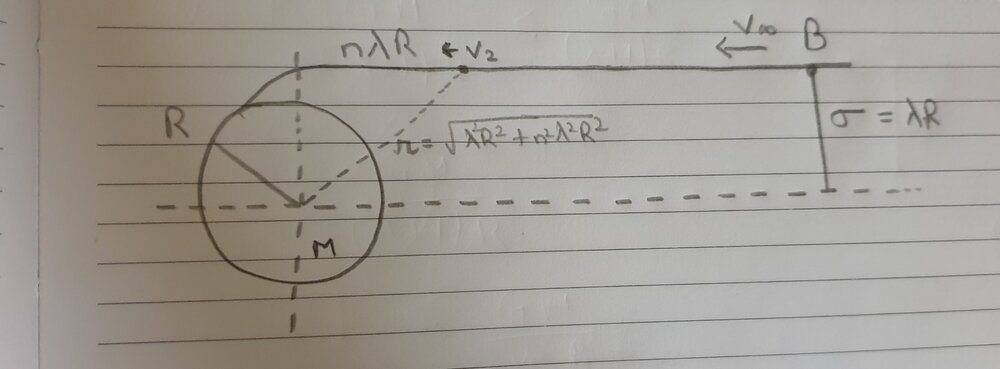
Since I need to find σ, I have assumed sigma to be an multiple of the radius ## R ##. So, let ## \sigma = \lambda R ##, where ## \lambda ## is some constant term. I have also assumed that the object ## B ## comes into the gravitational influence of object ## A ## when its a horizontal distance of ## n \lambda R ## away (n is some other constant term)
So, using Pythagoras theorem, the distance of object B ## r = \sqrt{{(\lambda R)}^2 + {(n \lambda R)}^2} ##. Substituting ## \sigma ## back, this implies ## r= \sigma \sqrt{n^2 + 1} ##
So, my approach is when object is at a distance ## r= \sigma \sqrt{n^2 + 1} ##, its velocity is ## v_2 ##.This velocity should be less than the orbital velocity at distance ## r ## for it to collide with planet A.
This velocity can be calculated using conservation of energy.
At infinity, ## T_0 = \frac{1}{2}m{v_{\inf}}^2 ##.
At point ## v_2 ##, ## T_1 = \frac{1}{2}m{v_2}^2 - \frac{GMm}{r} ##
Solving this we get ## {v_2}^2 = {v_{inf}}^2 + \frac{2GM}{r} ##. Since ## v_2 < v_{orb} ##
$$ \Rightarrow {v_{inf}}^2 + \frac{2GM}{r} < \frac{GM}{r} $$.
$$ \Rightarrow {v_{\inf}}^2 < - \frac{GM}{r} $$
$$ \Rightarrow r < - \frac{GM}{{v_{\inf}}^2} $$
Substituting everything, I get a value for ## \sigma ## which has the constant term ## n ##. However, I'm not supposed to have ## n ## in the answer. What am I doing wrong?
celestial body ASo this is the original figure of the problem.
Since I need to find σ, I have assumed sigma to be an multiple of the radius ## R ##. So, let ## \sigma = \lambda R ##, where ## \lambda ## is some constant term. I have also assumed that the object ## B ## comes into the gravitational influence of object ## A ## when its a horizontal distance of ## n \lambda R ## away (n is some other constant term)
So, using Pythagoras theorem, the distance of object B ## r = \sqrt{{(\lambda R)}^2 + {(n \lambda R)}^2} ##. Substituting ## \sigma ## back, this implies ## r= \sigma \sqrt{n^2 + 1} ##
So, my approach is when object is at a distance ## r= \sigma \sqrt{n^2 + 1} ##, its velocity is ## v_2 ##.This velocity should be less than the orbital velocity at distance ## r ## for it to collide with planet A.
This velocity can be calculated using conservation of energy.
At infinity, ## T_0 = \frac{1}{2}m{v_{\inf}}^2 ##.
At point ## v_2 ##, ## T_1 = \frac{1}{2}m{v_2}^2 - \frac{GMm}{r} ##
Solving this we get ## {v_2}^2 = {v_{inf}}^2 + \frac{2GM}{r} ##. Since ## v_2 < v_{orb} ##
$$ \Rightarrow {v_{inf}}^2 + \frac{2GM}{r} < \frac{GM}{r} $$.
$$ \Rightarrow {v_{\inf}}^2 < - \frac{GM}{r} $$
$$ \Rightarrow r < - \frac{GM}{{v_{\inf}}^2} $$
Substituting everything, I get a value for ## \sigma ## which has the constant term ## n ##. However, I'm not supposed to have ## n ## in the answer. What am I doing wrong?
Attachments
Last edited: