Gravitational Bending of Light: Equation for Photon Trajectory in Strong Fields

[kevindin]

I'm looking for an expression for the deflection of light in a static gravitational field.
Referring to 'deflection of star light past the sun' in Sean Carroll's "Spacetime and Geometry" - equation 7.80 for the "transverse gradient":

<br /> \nabla\perp\phi = \frac{GM}{(b^2 + x^2)^{3/2}}\vec b<br />

Deflection angle is

<br /> \alpha = {2GMb} \int {\frac{dx}{(b^2 + x^2)^{3/2}}}<br /> = \frac{4GM}{b}<br />

As far as I understand it, this is only valid for weak fields/small deflection. I'd like to plot photon paths in strong fields (with just a single point mass, not distributed), so I'm looking for the instantaneous deflection, which I'll plot/integrate numerically, based on mass, radial distance from mass, and angle of photon trajectory. It should not use the Schwarzschild metric, because I don't want the singularity at r=R_s and it only needs to be in 2 dimensions, because of spherical symmetry. So, is there an expression for the polar coordinates r2, θ2 and trajectory a2, for a photon traveling from p1 to p2, using M, r1, θ1, a1, L?
I've attached a diagram which I hope illustrates it:

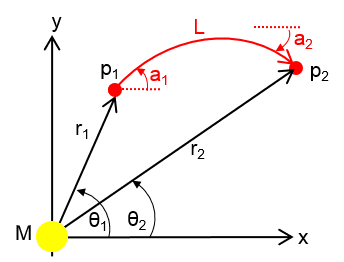
Many thanks
Kevin

 

[Ibix]

This thread may be of interest: https://www.physicsforums.com/threads/null-geodesics-in-schwarzschild-spacetime.895174/

Note that I didn't get the maths right until further down the page, so do read the whole thread.

 

[PeterDonis]

As far as I understand it, this is only valid for weak fields/small deflection.

It also only tells you the deflection angle "at infinity"--i.e. the total change in direction of the photon over the whole process of flying in, passing the gravitating body, then flying out again. It doesn't tell you anything about the path at finite distances from the gravitating body.

It should not use the Schwarzschild metric, because I don't want the singularity at r=R_s

What you mean is that you don't want to use Schwarzschild coordinates; in other coordinates (e.g., Painleve or Eddington-Finkelstein), there is no coordinate singularity at the horizon. But the geometry is the same. However, the thread @Ibix linked to uses Schwarzschild coordinates, so it only works outside the horizon.

 

[Ibix]

However, the thread @Ibix linked to uses Schwarzschild coordinates, so it only works outside the horizon.

It should be just a matter of transforming the coordinates to get a revised set of differential equations in terms of more useful coordinates, I think.

 

[kevindin]

It should be just a matter of transforming the coordinates to get a revised set of differential equations in terms of more useful coordinates, I think.

That's what I'm not confident of - my maths is a bit rusty. Someone must have done this already.

 

[PeterDonis]

It should be just a matter of transforming the coordinates to get a revised set of differential equations in terms of more useful coordinates, I think.

Actually, that by itself won't work, if you want to cover the region below the horizon. The problem is that, below the horizon, there is no timelike Killing vector field, so the whole mechanism used to derive the equations in that previous thread doesn't work, since it depends on energy at infinity being a constant of geodesic motion, and that's only true if there is a timelike Killing vector field. (The spacelike KVFs that make angular momentum a constant of the motion are still present below the horizon, though, so, counterintuitively, angular momentum is still well defined in that region even though energy at infinity is not.)

So a different method of solution is required for trajectories below the horizon. I have not seen one in the literature I have read, except for the special case of radial geodesics, which obviously won't cover the cases the OP is interested in.

 

[kevindin]

Is it possible to use the Kruskal-Szekeres metric? My gut feeling is yes, but I'm not sure of how to transform it into the expression I'm looking for.
Thanks

 

[Ibix]

You aren't changing metric, you're changing coordinates. You can use any coordinates you like but, as Peter says (and I should have realized), you have to go back to the geodesic equations. You can't adapt my approach because it relies on an assumption that isn't valid below the horizon. You can still use that L is a constant, but that may not be a lot of help.

 

[pervect]

Actually, that by itself won't work, if you want to cover the region below the horizon. The problem is that, below the horizon, there is no timelike Killing vector field, so the whole mechanism used to derive the equations in that previous thread doesn't work, since it depends on energy at infinity being a constant of geodesic motion, and that's only true if there is a timelike Killing vector field. (The spacelike KVFs that make angular momentum a constant of the motion are still present below the horizon, though, so, counterintuitively, angular momentum is still well defined in that region even though energy at infinity is not.)

So a different method of solution is required for trajectories below the horizon. I have not seen one in the literature I have read, except for the special case of radial geodesics, which obviously won't cover the cases the OP is interested in.

I think the equations will work, it's just that their interpretation changes. There is still a Killing vector field below the horizon, but it changes nature from time-like to space-like. I don't think this makes any difference to the mathematical equations of motion, the inner product of the tangent vector of the geodesic and the Killing vector field still remains constant along the geodesic. The physical interpretation of the significance of this becomes unclear, the conserved quantity is no longer an energy below the event horizon.

 

[PeterDonis]

There is still a Killing vector field below the horizon, but it changes nature from time-like to space-like. I don't think this makes any difference to the mathematical equations of motion, the inner product of the tangent vector of the geodesic and the Killing vector field still remains constant along the geodesic.

Hm, yes, good point.