- #1
Debo Industry
- 8
- 0
How did we measure the gravitational constant G = 2.034 x 10 ^ 17 cm ^ 2 and the Earth average density (specific gravity) p = 3.45 g / cm ^ 2 s ^ 2.
PhysicoRaj said:The gravitational constant was measured by Henry Cavendish, using a setup, like this:
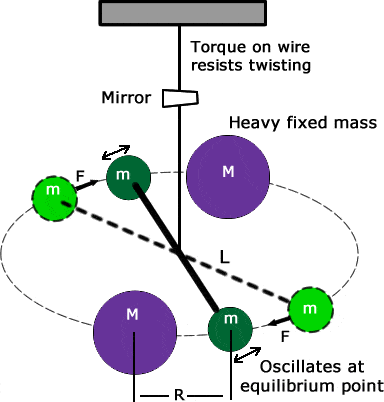
When the lead spheres are moved the gravitational force acting on the other set of spheres induces a force on the wire which twists, and the restoring torque can be equated to the gravitational force as follows:
torque = force * length
τθ=GMm/r2]*l
(where l is the length of bar, τ is the torque per unit angle of twist, θ is the angle of twist caused by the force).
So,
G=τθr2/Mml
θ, angle of twist can be measured by many methods.( in the figure it is measured by laser, and hence u see a mirror).
The Gravitational Constant, denoted by the symbol G, is a fundamental constant in physics that represents the strength of the gravitational force between two objects. It is an important factor in determining the force of gravity between any two masses.
The Gravitational Constant is typically measured using a device called a Cavendish balance, which measures the tiny gravitational force between two small masses. This force is then used to calculate the value of G. Other methods, such as using pendulums or measuring the deflection of light, can also be used to measure G.
The Gravitational Constant is important because it allows us to understand and quantify the force of gravity between objects. It is a key factor in many important equations, such as Newton's Law of Universal Gravitation and Einstein's Theory of General Relativity. It also helps us to understand the behavior of celestial bodies, such as planets and stars.
The Gravitational Constant has been measured to have a very precise value, but it is possible that it may have varied over time. Some theories propose that the value of G may have been different in the early universe, but more research is needed to confirm this.
The most recent accepted value of the Gravitational Constant, as determined by the National Institute of Standards and Technology (NIST), is 6.67430(15) x 10^-11 m^3 kg^-1 s^-2. This value has a relative uncertainty of 0.000000003%. However, there is ongoing research and debate in the scientific community about the exact value of G and whether it may need to be adjusted in the future.