Gre.al.12 transformation!of a function

[karush]

$\tiny{gre.al.12}$
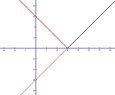
The graph of $y=\left|x-6\right|$
is is the standard $(x,y)$ coordinate plane.
Which of the following transformations. when applied to the graph of
$y=\left|x\right|$, in the graph of $y=\left|x-6\right|$?

a. Translation to the right 6 coordinate units
b. Translation to the left 6 coordinate units
c. Translation up 6 coordinate units
d. Translation down 6 coordinate units
e. Reflection across the line $x=6$

Spoiler: responder

ok chose a. Translation to the right 6 coordinate units
since we are only talking about changes in x and the minus sign will move the graph to the right

well probably a better way to explane this

 

[skeeter]

Think of $|x-6|$ as the distance (note distance is always $\ge$ zero) between $x$ and $6$ ...

$x=6 \implies |6-6| = 0$, the vertex of the transformed function $y = |x|$,hence the horizontal shift to the right.


Another way to visualize the transformation is to sketch the graph of $y = x - 6$, and reflect the part of the graph below the x-axis above the x-axis ...



btw, this graphing method works with any real-valued absolute value function

 

[karush]

i used the abs on desmos to ck it
but i think many people transform the wrong direction by impulse