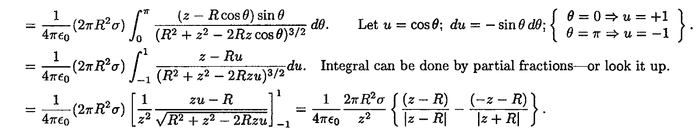SUMMARY
The discussion centers on solving a complex integral using integration by parts and partial fractions, specifically addressing the integral of the form integral (z du / (R² + z² - 2 Rz u) ^3/2). Participants clarify that integration by parts is the appropriate method for this integral, particularly when dealing with non-integer exponents. The conversation highlights the need for clear substitution techniques and the importance of using LaTeX for better readability in mathematical expressions.
PREREQUISITES
- Understanding of integration techniques, specifically integration by parts.
- Familiarity with partial fractions and their application in integrals.
- Basic knowledge of calculus, particularly regarding non-integer exponents.
- Proficiency in LaTeX for formatting mathematical expressions.
NEXT STEPS
- Research the application of integration by parts in complex integrals.
- Study the method of partial fractions for integrals involving non-integer exponents.
- Learn LaTeX to effectively present mathematical solutions and integrals.
- Explore advanced calculus topics related to substitutions in integrals.
USEFUL FOR
Mathematicians, calculus students, and anyone involved in solving complex integrals, particularly those interested in integration techniques and mathematical notation.