Griffiths Quantum Mechanics 2nd edition Chapter 8 equation is confusing

[edfink1]

Homework Statement

Griffiths Quantum Mechanics 2nd edition

Relevant Equations

Griffiths second edition equations 8.24 and 8.25

In Griffiths Quantum Mechanics 2nd edition, in Chapter 8 he calculates the following integral on page 323

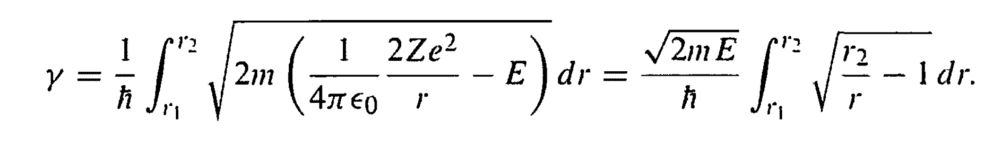
and he gets

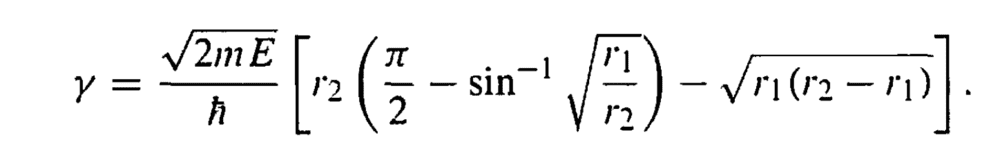
I disagree with this result, I think the integral should be

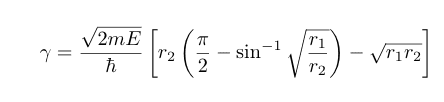
since

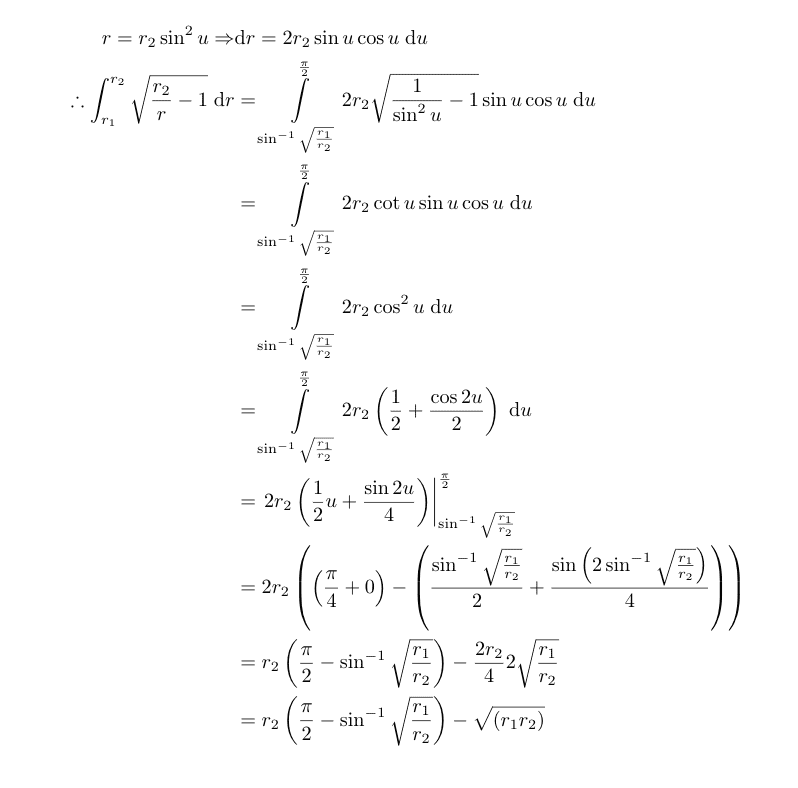
Maybe somebody can explain why I am wrong? Also, from equation 8.24 to 8.25, he makes the assumption that sinϵ ≅ ϵ, but how does that imply sin^(-1)ϵ ≅ ϵ, which seems to be what he assumes to get from 8.24 to 8.25. Any insight is greatly appreciated!

 

[TSny]

I disagree with this result, I think the integral should be
View attachment 270765

Note that the integral must go to zero as $r_2$ approaches $r_1$. But your result doesn't satisfy this condition.

Check the following:

Also, from equation 8.24 to 8.25, he makes the assumption that sinϵ ≅ ϵ, but how does that imply sin^(-1)ϵ ≅ ϵ, which seems to be what he assumes to get from 8.24 to 8.25. Any insight is greatly appreciated!

Take the inverse sine of both sides of sinϵ ≅ ϵ. Or, do a Taylor series of $\sin^{-1} x$ about $x=0$ .

 

[edfink1]

Thank you, I get it now!