Half Atwood machine: acceleration after inital force

[arturo]

Homework Statement

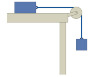
Assume that the block on the table (Figure 1) has twice the inertia of the hanging block.

(a)You give the block on the table a push to the right so that it starts to move. If the magnitude of the frictional force exerted by the table on the block is half the magnitude of the gravitational force exerted on the hanging block, what is the acceleration of the hanging block after you have stopped pushing the block on the table?

(b)What would this hanging-block acceleration be if you had pushed the block on the table to the left instead? Consider only a short time interval after you stop pushing.

Homework Equations

F_net = ma
F_g = mg

The Attempt at a Solution

I did get an answer to part(a). I solved as follows
F_table = T - .5mg = 2ma
F_mass = T - mg = -ma
(set equations equal to T)
-ma + mg = 2ma + .5mg
-a + g = 2a + .5g
3a = .5g
a = 1/6g

And that was correct. I assumed the initial force to get the system moving had no part to play in the equations.
When I looked at part(b), I thought it would be the exact same, the forces in my equations had not changed even though there was a initial force in the -x direction that was no longer present. However, the answer is not the same, and I don't understand how that momentary initial force impacts the final acceleration.

please advise,
arturo

 

[TSny]

When I looked at part(b), I thought it would be the exact same, the forces in my equations had not changed

Does each force in part (b) still have the same direction as in part (a)?

 

[arturo]

Friction changes signs when the force is applied in the opposite direction on the table block, and I would be lead to assume that that stays facing the opposite direction even after the force is no longer applied.

If that’s the case, then:
-a + g = 2a - .5g
3a = 1.5g
a = .5g

Which is correct.

For a moment I did not understand why the frictional force wouldn’t flip back the moment the force on the table block was no loner exerted. After reconsidering the problem, that would be because within that short time interval after the force is removed, it would still have velocity in the -x direction (as friction opposes motion, not force), correct?

Thank you for your assistance.

 

[TSny]

For a moment I did not understand why the frictional force wouldn’t flip back the moment the force on the table block was no loner exerted. After reconsidering the problem, that would be because within that short time interval after the force is removed, it would still have velocity in the -x direction (as friction opposes motion, not force), correct?

Yes. Good work.