Atwood's Machine: Understanding Acceleration and Tension

[FScheuer]

Homework Statement

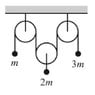
There is an Atwood machine (image attached) with 3 masses, m, 2m, and 3m.

Homework Equations

What is the acceleration of each mass?

The Attempt at a Solution

[/B]
I’m not quite sure where to start here. I know that there is a gravitational force downward on each mass, mg, 2mg, and 3mg respectively. I also know that tension is pulling each of the masses upward. I think I would be able to begin solving the problem if I understood how the force of tension in the string was applied to each mass. Is the force of tension on each mass different?

 

[Orodruin]

If you can neglect friction and the pulleys are massless, the tension is the same in the entire string. What you need to do is to start making free body diagrams to your heart's delight. You will also need a constraint to keep the string length constant.

 

[FScheuer]

If you can neglect friction and the pulleys are massless, the tension is the same in the entire string. What you need to do is to start making free body diagrams to your heart's delight. You will also need a constraint to keep the string length constant.

I set it all up and got .5g upward for the acceleration of the first two masses and .5g downward for the acceleration of the third. Does that seem correct?

 

[haruspex]

I set it all up and got .5g upward for the acceleration of the first two masses and .5g downward for the acceleration of the third. Does that seem correct?

With those numbers, the string is getting longer at 1g. The first three lengths each get shorter at .5g while the last gets longer at .5g.
Please post your working.

 

[FScheuer]

With those numbers, the string is getting longer at 1g. The first three lengths each get shorter at .5g while the last gets longer at .5g.
Please post your working.

I set up three equations for the accelerations.

a1 = (mg + T)/m

a2 = (2mg + 2T)/2m

a3 = (3mg + T)/3m

I’m not quite sure how to use the constant string length as a constraint. Before I set a1 equal to a3 but I now realize that they are not necessarily equal.

 

[Orodruin]

I’m not quite sure how to use the constant string length as a constraint.

Write the total string length as a function of the displacement of the pulleys and differentiate it twice.

 

[FScheuer]

Write the total string length as a function of the displacement of the pulleys and differentiate it twice.

What exactly do you mean by that? Isn’t the total string length constant?

 

[Orodruin]

What exactly do you mean by that? Isn’t the total string length constant?

Yes. But it can also be expressed in terms of the displacements. This is the entire point. What happens when you differentiate a constant? What do you get out when you differentiate the displacements twice?

Since you have only three equations and four variables (the accelerations and the tension), you need this additional condition to solve the system.

 

[Chestermiller]

Express the length of string (aside from the parts in contact with the pulley) as $L=L_1+2L_2+L_3$. Differentiate this twice with respect to time to get a relationship between the accelerations of the three masses.

 

[FScheuer]

Yes. But it can also be expressed in terms of the displacements. This is the entire point. What happens when you differentiate a constant? What do you get out when you differentiate the displacements twice?

Since you have only three equations and four variables (the accelerations and the tension), you need this additional condition to solve the system.

I added the equation and then solved to get -1/5mg for the first two masses, and 3/5mg for the third. This seems to match up with the answer I found online. Thanks.

 

[Orodruin]

I added the equation and then solved to get -1/5mg for the first two masses, and 3/5mg for the third. This seems to match up with the answer I found online. Thanks.

It is also the same result as I got (assuming that you define the positive direction to be down for all masses, which agrees with your sign for the gravitational term in post #5, but note that you have defined $T$ to be negative of the tension in the string as positive $T$ in those equations would lead to the tension accelerating the masses downwards too - of course this does not matter for the solution if you only solve for the accelerations, but it will matter if you are interested in the string tension).