Trisztan
- 6
- 1
- Homework Statement
- What is the voltage around a conducting ring of diameter ##l##, moving through a uniform magnetic field of magnitude ##B##, at speed ##v##?
- Relevant Equations
- Definition of potential difference:
$$\Delta V = -\int_i^f {\mathbf{E}\cdot \mathrm{d}\mathbf{s}}$$
Force magnitude equivalence under the Hall effect:
$$qE = qvB$$
This is the diagram provided in the question:
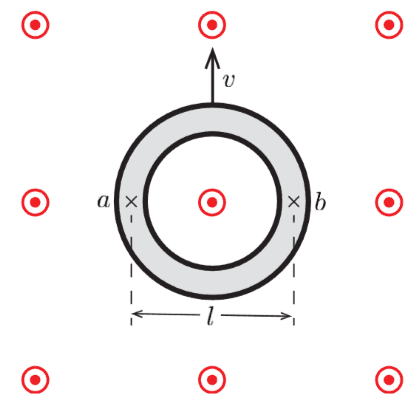
The ring is made of conducting material. I was originally asked to find the potential difference between ##a## and ##b##. I did so using the Hall effect (and assuming it would work as per normal in this situation). This got me ##\Delta V = vBl##.
However, I am now lost on how to find the "voltage around the ring". If I had to guess, I would say its 0 everywhere around the ring except at either ##a## and ##b## (depending on which you take to be the point where ##V=0##).
Any help would be much appreciated.
The ring is made of conducting material. I was originally asked to find the potential difference between ##a## and ##b##. I did so using the Hall effect (and assuming it would work as per normal in this situation). This got me ##\Delta V = vBl##.
However, I am now lost on how to find the "voltage around the ring". If I had to guess, I would say its 0 everywhere around the ring except at either ##a## and ##b## (depending on which you take to be the point where ##V=0##).
Any help would be much appreciated.