Hanging pith balls on a thread...charge, Fg, Fe and tension

[Brittany Anderson]

Homework Statement

Two pith balls each have a mass of 1.0g and equal charges. One pith ball is hung from an insulating thread. The other is fixed at a horizontal distance of 3.0cm from the first, The first hangs at an angle of 30.0° from the vertical. Find:
a) the gravitational force on the hanging pith ball
b) the electric force on the hanging pith ball
c) the charge on each of the balls
d) the tension in the thread

m=0.001kg
dx=0.03 m
θ=30°

Homework Equations

g=Fg/m
Fe=kq1q2/r^2
E=Fe/q
E=ΔV/Δd
ΔV=ΔEp/q

(all of these should have vectors except for the last equation! I didn't know how to put vectors on.. sorry

The Attempt at a Solution

SO. We know from the problem,
m=0.001kg
dx=0.03 m
θ=30°

a) if I'm not mistaken, in order to find Fg we must use g=Fg/m or when rearranged mg=Fg
If we use this, we can determine that the Fg= (0.001kg)(9.81m/s^2)
Which would give us 0.00981 as an answer for Fg.. correct?

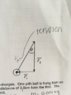
b) For this one I'm at a bit of a loss.. Based on formulas we don't exactly have one that matches. I have made a triangle however and so I'm wondering if this was the right of executing it... Please view the insert below on the triangle. If I used tan(30)=Fe/Fg or 0.00981tan(30)= Fe, would that work? does the triangle even correspond or make sense in this scenario??

c) for charges, I am assuming that I rearrange the Fe=kq1q2/r^2 formula to find the charges.. as in Fe⋅r^2/k= q1q2 and then just divide by 2 tog et each of the charges because they are equal?

d) For tension, do I use the triangle again with c^2=a^2+b^2 rule?

Please just help me confirm because I might have this all wrong :) Hope all my attempts are clear and make sense! Let me know! Thanks in advance.

 

[tnich]

First of all, please use LaTeX to write your equations. It's easy and it makes it a lot more likely that someone will respond to your posts.

Which would give us 0.00981 as an answer for Fg.. correct?

This part looks good.

b) For this one I'm at a bit of a loss.. Based on formulas we don't exactly have one that matches. I have made a triangle however and so I'm wondering if this was the right of executing it... Please view the insert below on the triangle. If I used tan(30)=Fe/Fg or 0.00981tan(30)= Fe, would that work? does the triangle even correspond or make sense in this scenario??

You have the right approach here. You have done vector addition to get the resultant force on the pith ball. That is, you drew the vectors nose-to-tail. I'm not sure if you knew you were graphically adding the vectors. You have correctly written the equation relating the two vectors to the direction of the resultant force vector and you can solve it to find the electric force on the hanging pith ball.

c) for charges, I am assuming that I rearrange the Fe=kq1q2/r^2 formula to find the charges.. as in Fe⋅r^2/k= q1q2 and then just divide by 2 tog et each of the charges because they are equal?

This is almost right, but think of it this way. Both pith balls have the same charge $Q$. So $q_1=Q$ and $q_2=Q$. Substitute Q for $q_1$ and $q_2$ in your equation for $F_e$. Now you have a $Q^2$. How would you solve for Q?

d) For tension, do I use the triangle again with c^2=a^2+b^2 rule?

Yes.

 

[haruspex]

then just divide by 2 tog et each of the charges because they are equal?

That would make sense if the equation were Fe⋅r^2/k= q1+q2, but it is Fe⋅r^2/k= q1q2.