Height of a fluid in a small tube

[Ampere]

Homework Statement

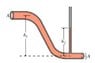
An upper tube of cross sectional area A, atmospheric pressure, and height h₁ is connected to a lower tube with cross sectional area A/2 (and height 0). A fluid of uniform density rho flows through the system, with velocity v measured in the upper tube. A small open tube branches up off the lower one, with a column of fluid of height h₂ inside it. Find h₂.

(See attached diagram.)

Homework Equations

Bernoulli's equation,

P₁ + pgh₁ +1/2*pv₁² = constant

Continuity equation,

A₁v₁ = A₂v₂

The Attempt at a Solution

Applying Bernoulli's equation between the top of fluid of height h₂ and the left endpoint of the system, I got:

(point 1 = left endpoint, point 2 = top of the column with height h₂)

P₁ = atmospheric
P₂ = atmospheric
KE₁ = 1/2*rho*v²
KE₂ = 0
PE₁ = rho*g*h₁
PE₂ = rho*g*h₂

Therefore h₂ = h₁ + v²/(2g). Is this right? I would think that a faster moving fluid pushes h₂ up even higher (with h₂ = h₁ when v=0).

The continuity equation tells us that the speed of the fluid inside the smaller tube is 2v. But does this even matter?

 

[tiny-tim]

Welcome to PF!

Hi Ampere! Welcome to PF!

Applying Bernoulli's equation between the top of fluid of height h₂ and the left endpoint of the system …

No, you can't do that … Bernoulli's equation only applies along a streamline …

and the streamline doesn't go up that little tube, does it? ​

The continuity equation tells us that the speed of the fluid inside the smaller tube is 2v. But does this even matter?

Yes, because that is in the streamline!

 

[Ampere]

Thanks. So in that case you can find the pressure right under the small tube (with height h₂ - did this below). But what equation do I use to travel outside the streamline?

P₁ = atmospheric
P₂ = unknown
KE₁ = 1/2*rho*v²
KE₂ = 1/2*rho*(2v)²
PE₁ = rho*g*h₁
PE₂ = 0

So P₂ = P_atm + rho*g*h₁ - 3/2*rho*v²

 

[tiny-tim]

Hi Ampere!

Thanks. So in that case you can find the pressure right under the small tube (with height h₂ - did this below). But what equation do I use to travel outside the streamline?

The fluid in the thin vertical tube is stationary, so just use pressure difference = ρgh

(technically, you can use any line in a stationary fluid as a streamline … but that doesn't mean you can then tag it onto a "real" streamline in a moving part of the fluid )

 

[Ampere]

So I get

dP = rho*g*h₂
P₂ - P_atm = rho*g*h₂

and

h₂ = h₁ - 3v²/(2g)

So the faster the fluid flows, the lower the height h₂ is? Is there actually a flow rate which would make h₂ = 0, or even less than 0?

 

[tiny-tim]

So the faster the fluid flows, the lower the height h₂ is?

Bernoulli's equation does mean that when the speed is faster the pressure is lower.

Is there actually a flow rate which would make h₂ = 0, or even less than 0?

work it out!

 

[Ampere]

I found that the speed at which h₂=0 is √(2gh₁/3).

So if h₁ = 1m, then v = 2.556 m/s. What if I had v = 3 m/s, or even 6 m/s? What would be the physical meaning of a negative height?

For example, if we go with h₁ = 1m and v = 6 m/s, we get h₂ = -4.51m. Huh?

 

[tiny-tim]

What would be the physical meaning of a negative height?

It would mean you have a vacuum pump!

 

[Ampere]

Ah so air would be sucked into the tube along with the fluid? Interesting!

Thanks, this makes sense now.