LCKurtz said:
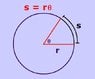
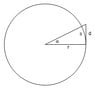
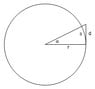
The picture is below. You are given ##h,~H,~r,\text{ and } d= u+v##. So ##\alpha = \arccos\frac r {r+h}## and ##u = r\alpha##. So ##v = d -u## and ##\beta = \frac v r##. Then ##\frac {r+x} r = \sec\beta## so
##x =r\sec\beta - r## and ##y = H-x##. Just plug in the numbers as you go.
View attachment 215338
Yes, thank you. That works quite well. However, another given would have to be either
d or
v, since we only know the value of
u and
v = d-u contains
two unknown values. At least, I couldn't go any further until I plugged in a value for
v. Using
h = 6/5280 miles,
r = 3960 miles, and
H = 200/5280 miles, I got
y = 103.99963 feet. Using the Pythagorean method, I got
y = 104.00022 feet, a difference only
0.0006 feet, which is negligible. Your method appears to be quicker and does avoid square roots.
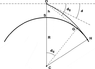
But, there does seem to be a problem here. Calculating the distance from the observer to the island using arc length only takes into account the distance along the surface (
abc in the diagram below), not the line-of-sight distance (
dbe). The line dbe is longer than the arc
abc, although in models such as this, where
r is very large and
h, x, y and
H are very small, it hardly makes any difference. But I think I'll stick with the Pythagorean method for this type of problem, because it involves straight lines of sight (not including refraction).
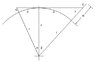
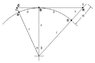
Plus, I had to prove to myself (informally, at least - see illustration below) that a line of sight tangential to the horizon, from an observer above the surface of the Earth to a distant object just visible above the horizon (and above the Earth's surface), is longer that the arc length along the surface to the bases of the two points. My guess is that the line of sight is longer than the length of the arc along the surface. In other words, if you "unbent" arc
ab into a straight line, it would be shorter than line
cd.
![IMG_E1770[1].JPG](/data/attachments/197/197245-e7c4ca7ce4c9690732b95ad63c4731eb.jpg?hash=58TKfOTJaQ)