Height of an island beyond the horizon

[fizixfan]

Homework Statement

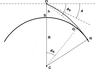
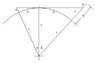
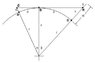
If I am standing on the ocean shore, and my eye level is 6 feet above sea level, how far above the horizon would an island appear that is 15 miles away and whose highest point is 200 feet above sea level (assuming the earth’s diameter is 3,960 miles?) In other words, how many feet would the island extend above my line of sight, i.e., I would see the top “x” feet of the island, not accounting for atmospheric distortion or diffraction.

Homework Equations

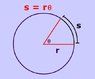
the calculation for "horizon drop”
h = (SQRT(d^2+R^2)-R) where
h = horizon drop
R = Radius of Earth
d = Distance from Observer

The Attempt at a Solution

h = ((SQRT(d1^2+R^2)-R))-((SQRT(d2^2+R^2)-R))-

 

[mfb]

h = ((SQRT(d1^2+R^2)-R))-((SQRT(d2^2+R^2)-R))-

What did you calculate here, why, and what was the result?

Did you draw a sketch?

 

[fizixfan]

What did you calculate here, why, and what was the result?

Did you draw a sketch?

Yes, I did, and it's NOT TO SCALE. It's actually much faster and much easier to do the calculations by hand. So, Height of observer = 6 ft, distance to horizon = 3.0 miles (calculations on left side of sketch). So distance from horizon to island = 15-3 = 12 miles. Horizon drop at distance of 12 miles = 96.0 feet (calculations on right side of sketch). So, portion of island visible above horizon = 200-96 = 104 ft.

This may not be all tickety-boo, but I'm pretty sure it's right. I can use the same calculations to show that for an observer at a height of 3 feet, the horizon is 2.12 miles away, so it's 12.88 miles from the horizon to the island, and the horizon drop for 12.88 miles is 110.6 feet, and the portion of the island visible above the horizon is 200-110.6 = 89.4 feet, which is 14.6 feet less of the island that would be visible from a height of 6 feet.

Why am I doing this? It's my way of proving empirically to myself that the world is indeed a globe. No proof is more satisfying than when you do it for yourself. I took two pictures of an island about 15 miles away from the seashore - one from a height of 6 feet, and one from a height of 3 feet. Not surprisingly, the island taken from a height of 3 feet appeared closer to the horizon than the one taken from a height of 6 feet. I did this partly in response to all the flat-earthers out there who say there is no proof, that we've been lied to all along. Of course, I don't believe them - I think they're seriously misguided, but that's the beautiful thing about the scientific method - it works. The world is round! I had to prove to myself, since I never really had before.

Feel free to criticize my methods, but feel just as free to prove me wrong!

 

[haruspex]

h = (SQRT(d^2+R^2)-R) where
...
h = ((SQRT(d1^2+R^2)-R))-((SQRT(d2^2+R^2)-R))-

Not sure what h represents in the second equation. It is clearly different from the h in the first equation.
I cannot think why you would want to take the difference of the two terms on the right. It does not seem to be what you did in your calculation. Rather, you did
$h_{vis}=h_{act}-h_{hid}$
$h_{hid}=\sqrt{R^2+d_2^2}-R$
$d_2=d_{tot}-d_1$
$d_1=\sqrt{(R+h_1)^2-R^2}$
Since R is so much larger than the other variables, you can approximate $\sqrt{(R+x)^2-R^2}$ as $\sqrt{2Rx}$.
This gives $h_{hid}=\frac{(d_{tot}-\sqrt{2Rh})^2}{2R}$.

 

[fizixfan]

Not sure what h represents in the second equation. It is clearly different from the h in the first equation.
I cannot think why you would want to take the difference of the two terms on the right. It does not seem to be what you did in your calculation. Rather, you did
$h_{vis}=h_{act}-h_{hid}$
$h_{hid}=\sqrt{R^2+d_2^2}-R$
$d_2=d_{tot}-d_1$
$d_1=\sqrt{(R+h_1)^2-R^2}$
Since R is so much larger than the other variables, you can approximate $\sqrt{(R+x)^2-R^2}$ as $\sqrt{2Rx}$.
This gives $h_{hid}=\frac{(d_{tot}-\sqrt{2Rh})^2}{2R}$.

Did you see my post (above yours)? https://www.physicsforums.com/threads/height-of-an-island-beyond-the-horizon.930229/
I clarified what I was looking for, and solved the problem myself. Feel free to comment.

 

[haruspex]

Did you see my post (above yours)? https://www.physicsforums.com/threads/height-of-an-island-beyond-the-horizon.930229/
I clarified what I was looking for, and solved the problem myself. Feel free to comment.

Yes, I was just pointing out that your equation in post #1 is not what you did in post 3. It was unclear whether you realized that.
Also, I was trying to show the advantage of keeping everything symbolic until the end. Amongst other benefits, it makes the calculation both easier and more accurate.

 

[fizixfan]

Not sure what h represents in the second equation. It is clearly different from the h in the first equation.
I cannot think why you would want to take the difference of the two terms on the right. It does not seem to be what you did in your calculation. Rather, you did
$h_{vis}=h_{act}-h_{hid}$
$h_{hid}=\sqrt{R^2+d_2^2}-R$
$d_2=d_{tot}-d_1$
$d_1=\sqrt{(R+h_1)^2-R^2}$
Since R is so much larger than the other variables, you can approximate $\sqrt{(R+x)^2-R^2}$ as $\sqrt{2Rx}$.
This gives $h_{hid}=\frac{(d_{tot}-\sqrt{2Rh})^2}{2R}$.

Thanks for this. Please ignore my original equation, which is quite wrong.
With regard to your response, I'm not sure which "h" you're referring to in $h_{hid}=\frac{(d_{tot}-\sqrt{2Rh})^2}{2R}$
Do you mean
$h_{vis}$ or $h_{act}$?
I don't know which "h" to plug into the equation.

To me, all the variables are important, including the height of the observer, even if it's only 3 feet or 6 feet. You can see from the photograph that it does make a difference when a picture of and island 15 miles distant is taken at 3 feet and 6 feet above sea level. In those 3 feet of height difference, some islands disappear.

I use a step-wise method to calculate the height of a distant object above the horizon (hvis).

Assuming the radius of the Earth (R) is 3,960 miles (a very close approximation), and using the Pythagorean theorem, I calculated that the distance (d1) to the horizon, where ho is the height of the observer above sea level is d1 = sqrt((R+(ho/5280))^2-R^2) = 3.0 miles. So the distance from the horizon to the island is 15-3=12 miles (d2). Then I calculated the horizon drop (h1) at a distance of 12 miles, and got h1 = sqrt(R^2+d2^2)-R = 96.0 feet. So the portion of the island visible above the horizon = h2-h1=200-96=104 feet. Using the same calculations, I determined that the portion of the island visible above the horizon from an eye level of 3 feet asl was 89 feet - 15 feet less than from an eye level of 6 feet asl.

This may be somewhat inelegant, and forgive me for not using MathJax (in which I am not at all conversant), but I can plug these formulas into Excel and "mass produce" the results for any given observer height (ho), island distance (d1+d2) and island height (h2). So far, I haven't been able to calculate the "hvis", given only the height of the observer above sea level, distance from observer to island, and height of island above sea level, although I know there must be a way.

 

[fizixfan]

Did you see my post (above yours)? https://www.physicsforums.com/threads/height-of-an-island-beyond-the-horizon.930229/
I clarified what I was looking for, and solved the problem myself. Feel free to comment.

Here's something that makes the subject a little sexier :-) I did this in Excel.

 

[LCKurtz]

Normally, wouldn't you measure the distance from the observer to the island by the distance (arc length) along the surface between them? It makes the calculations much simpler (no square roots). Just a couple of trig functions. I get $h_{vis} = 194.8$ using your original numbers.
[Edit] Still checking this...
Correction: I get $104.01$. Pretty much agrees with you because the straight line distance and the curved distance are about equal in the big scheme of things. Another interesting calculation shows that if your eyelevel is 150 feet above the ground, that is the point at which you see the whole tower.

 

[Ophiolite]

I note that you have not accounted for refraction. (Beyond the scope of the original question, but important in practice.)

 

[fizixfan]

Normally, wouldn't you measure the distance from the observer to the island by the distance (arc length) along the surface between them? It makes the calculations much simpler (no square roots). Just a couple of trig functions. I get $h_{vis} = 194.8$ using your original numbers.
[Edit] Still checking this...
Correction: I get $104.01$. Pretty much agrees with you because the straight line distance and the curved distance are about equal in the big scheme of things. Another interesting calculation shows that if your eyelevel is 150 feet above the ground, that is the point at which you see the whole tower.

That's interesting - you got the same answer ( $h_{vis} = 104.1 ft$), presumably for an observer height of $6 ft$, a distance of $15 miles$ and a island height of $200 ft$. But I'm not sure how you calculated this by measuring the arc length between the island and the observer (or possibly the central angle). I know the basic equation is arc length = [radius • central angle (radians)] or arc length = circumference • [central angle (degrees) ÷ 360] where circumference = [2 • π • radius] but you'd have to already know the central angle to get this (wouldn't you?), and I can only get this by reverse-engineering my calculations, i.e., ##cosΦ = d₁/(R+h₂)## But I can't reproduce your results using the "s = r⋅θ" equation. Could you possibly show the calculations you used?

 

[fizixfan]

I note that you have not accounted for refraction. (Beyond the scope of the original question, but important in practice.)

You’re right, I haven’t. But there’s a rule of thumb for estimating atmospheric refraction. We can see farther due to refraction. On average, it’s the equivalent of living on a planet that is 1/7 larger, ie, with a radius of 4,620 miles. So, using all the same measurements I started out with, the the distance to the horizon from an observation height of 6 feet increases from 3 miles to 3.24 miles, and the hvis of the island would increase from 104 feet to 121 feet - an extra 17 feet if my calculations are correct.

 

[LCKurtz]

That's interesting - you got the same answer ( $h_{vis} = 104.1 ft$), presumably for an observer height of $6 ft$, a distance of $15 miles$ and a island height of $200 ft$. But I'm not sure how you calculated this by measuring the arc length between the island and the observer (or possibly the central angle). I know the basic equation is arc length = [radius • central angle (radians)] or arc length = circumference • [central angle (degrees) ÷ 360] where circumference = [2 • π • radius] but you'd have to already know the central angle to get this (wouldn't you?), and I can only get this by reverse-engineering my calculations, i.e., ##cosΦ = d₁/(R+h₂)## But I can't reproduce your results using the "s = r⋅θ" equation. Could you possibly show the calculations you used?

I will post a picture and the equations in the next day or so.

 

[Ophiolite]

You’re right, I haven’t. But there’s a rule of thumb for estimating atmospheric refraction. We can see farther due to refraction. On average, it’s the equivalent of living on a planet that is 1/7 larger, ie, with a radius of 4,620 miles. So, using all the same measurements I started out with, the the distance to the horizon from an observation height of 6 feet increases from 3 miles to 3.24 miles, and the hvis of the island would increase from 104 feet to 121 feet - an extra 17 feet if my calculations are correct.

Interesting. I was not aware of that approximation. I imagine it would be inappropriate for detailed surveying, but ideal for improving back of the envelope calculations.

 

[LCKurtz]

The picture is below. You are given $h,~H,~r,\text{ and } d= u+v$. So $\alpha = \arccos\frac r {r+h}$ and $u = r\alpha$. So $v = d -u$ and $\beta = \frac v r$. Then $\frac {r+x} r = \sec\beta$ so
$x =r\sec\beta - r$ and $y = H-x$. Just plug in the numbers as you go.

 

[fizixfan]

The picture is below. You are given $h,~H,~r,\text{ and } d= u+v$. So $\alpha = \arccos\frac r {r+h}$ and $u = r\alpha$. So $v = d -u$ and $\beta = \frac v r$. Then $\frac {r+x} r = \sec\beta$ so
$x =r\sec\beta - r$ and $y = H-x$. Just plug in the numbers as you go.
View attachment 215338

Yes, thank you. That works quite well. However, another given would have to be either d or v, since we only know the value of u and v = d-u contains two unknown values. At least, I couldn't go any further until I plugged in a value for v. Using h = 6/5280 miles, r = 3960 miles, and H = 200/5280 miles, I got y = 103.99963 feet. Using the Pythagorean method, I got y = 104.00022 feet, a difference only 0.0006 feet, which is negligible. Your method appears to be quicker and does avoid square roots.

But, there does seem to be a problem here. Calculating the distance from the observer to the island using arc length only takes into account the distance along the surface (abc in the diagram below), not the line-of-sight distance (dbe). The line dbe is longer than the arc abc, although in models such as this, where r is very large and h, x, y and H are very small, it hardly makes any difference. But I think I'll stick with the Pythagorean method for this type of problem, because it involves straight lines of sight (not including refraction).

Plus, I had to prove to myself (informally, at least - see illustration below) that a line of sight tangential to the horizon, from an observer above the surface of the Earth to a distant object just visible above the horizon (and above the Earth's surface), is longer that the arc length along the surface to the bases of the two points. My guess is that the line of sight is longer than the length of the arc along the surface. In other words, if you "unbent" arc ab into a straight line, it would be shorter than line cd.

 

[LCKurtz]

The picture is below. You are given $h,~H,~r,\text{ and } d= u+v$.

Yes, thank you. That works quite well. However, another given would have to be either d or v, since we only know the value of u and v = d-u contains two unknown values.

As I said in my post, you are given $d$ which equals $u+v$. Your original problem had $d = 15$.

 

[fizixfan]

I thought that was probably the case. But you didn’t address the second part of my post, which discusses whether the observer is viewing along the surface of an arc, or using line of sight from their vantage point.

 

[LCKurtz]

Plus, I had to prove to myself (informally, at least - see illustration below) that a line of sight tangential to the horizon, from an observer above the surface of the Earth to a distant object just visible above the horizon (and above the Earth's surface), is longer that the arc length along the surface to the bases of the two points. My guess is that the line of sight is longer than the length of the arc along the surface.

You don't have to guess. Look at the picture below. Calculate $d$ and $s$ in terms of the angle $\alpha$ and radius $r$. Can you see why $d>s$?

 

[LCKurtz]

I thought that was probably the case. But you didn’t address the second part of my post, which discusses whether the observer is viewing along the surface of an arc, or using line of sight from their vantage point.

I don't understand this question. You can't see around corners.

 

[fizixfan]

I don't understand this question. You can't see around corners.

You said, “Normally, wouldn't you measure the distance from the observer to the island by the distance (arc length) along the surface between them?”

 

[fizixfan]

You said, “Normally, wouldn't you measure the distance from the observer to the island by the distance (arc length) along the surface between them?”

I’m measuring the distance by line of sight, not by the distance along the surface. How far you can see is not the same as arc length - it’s a straight line.

 

[LCKurtz]

I’m measuring the distance by line of sight, not by the distance along the surface. How far you can see is not the same as arc length - it’s a straight line.

I understand how you are measuring the distance. It's your problem and you can do it any way you wish. I am just pointing out that the standard way to measure the distance between two points on Earth is along an arc on the surface between them. If the Earth were a perfect sphere these arcs would be on great circles. And, as you have noticed, for your particular calculation it doesn't make much difference.

 

[fizixfan]

I understand how you are measuring the distance. It's your problem and you can do it any way you wish. I am just pointing out that the standard way to measure the distance between two points on Earth is along an arc on the surface between them. If the Earth were a perfect sphere these arcs would be on great circles. And, as you have noticed, for your particular calculation it doesn't make much difference.

Fair enough. My apologies if I insulted you - it was uncalled for.

As for this (from post #19):

"Calculate d and s in terms of the angle α and radius r. Can you see why d>s?"

No, I tried but I can't see it. I could only prove it in one case (post #16), i.e., for α = 45°. I'm too old and rusty to do a general proof.

Thanks for your help though - I appreciate it.