Discussion Overview
The discussion revolves around solving heights and distances problems using trigonometry, specifically focusing on the application of the Law of Cosines and the construction of geometric diagrams to visualize the scenarios presented in the problems.
Discussion Character
- Homework-related
- Mathematical reasoning
- Technical explanation
- Debate/contested
Main Points Raised
- One participant expresses difficulty in visualizing the problems and understanding the ratios involved, indicating a potential language barrier affecting comprehension.
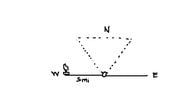
- Another participant suggests using diagrams to clarify the relationships between the variables, specifically asking for expressions of certain lengths in terms of height.
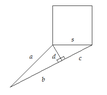
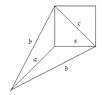
- A different approach is proposed involving the Law of Cosines, with participants discussing how to express various sides of triangles in terms of height and other variables.
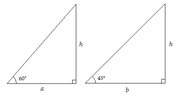
- One participant attempts to create multiple right triangles with different angles to analyze the height of a building, noting that they observe the heights remain constant across these triangles.
- There is a discussion about the angles involved in the triangles, with one participant questioning the assumption of a 90-degree angle in a specific scenario.
- Several participants engage in deriving equations based on the Law of Cosines, with varying degrees of success and clarity, leading to some confusion about the relationships between the variables.
- One participant expresses uncertainty about how to proceed after substituting values into their equations, leading to further clarification requests from others.
- Another participant suggests using the double angle identity for cosine to simplify their equations, while others express confusion about the introduction of sine into their calculations.
- There is a back-and-forth regarding the correctness of derived expressions and the necessity of finding numeric values versus keeping the expressions in terms of variables.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the best approach to solve the problems, with multiple competing views on how to apply trigonometric principles and the Law of Cosines. Some participants express confusion and seek clarification, indicating that the discussion remains unresolved.
Contextual Notes
Participants reference specific angles and relationships in their diagrams, but there are unresolved assumptions regarding the configurations of the triangles and the angles involved. Some mathematical steps are not fully clarified, leading to potential gaps in understanding.