Helmholtz theorem derivation question

[DivergentSpectrum]

http://en.wikipedia.org/wiki/Helmholtz_decomposition#Derivation
how do we go from

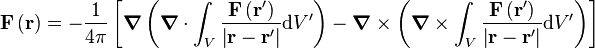
to

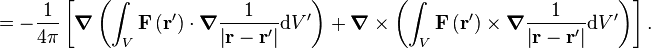
also on the next step

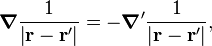
∇' just means the gradient with respect to r', right?
Also, why do i have to use the dirac delta function? i thought it was only used to deal with discontinuities?

also when we say

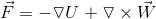
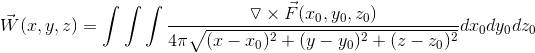
the volume integral of a vector field just means we do the triple integral on each component of the vector field independently right?

 

[jedishrfu]

I think they're using a vector identity to slide the del inside the integral:

http://en.m.wikipedia.org/wiki/Del

 

[DivergentSpectrum]

del is an operator though? if i applied that to this case then id get stuff like

or

i don't know why theyd explain each step then leave one completely mising