Stokes Theorem: Vector Integral Identity Proof

[Master1022]

TL;DR Summary

It is a proof question, but I am struggling to understand what steps I should take next

Hi,

My question pertains to the question in the image attached.

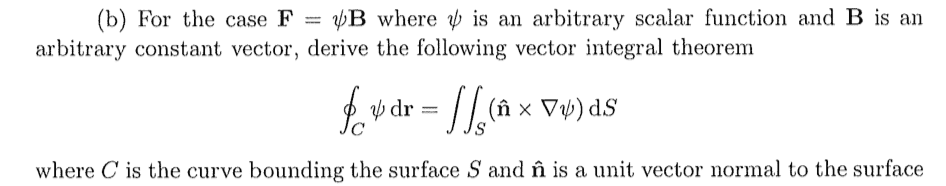
My current method:
Part (a) of the question was to state what Stokes' theorem was, so I am assuming that this part is using Stokes' Theorem in some way, but I fail to see all the steps.

I noted that $$\nabla \times \vec F = \nabla \times (\psi \vec B) = \psi \left( \nabla \times \vec B \right) - \vec B \times \nabla \psi$$
Then I thought that $\nabla \times \vec B = \vec 0$ as $\vec B$ is a constant vector. Simplifying the above expression, we are left with:
$$\nabla \times \vec F = - \vec B \times \nabla \psi$$ Then I attempted to include the normal vector $\hat n dS$ by 'dotting' both sides with it:
$$\left( \nabla \times \vec F \right) \cdot \hat n dS = \left( - \vec B \times \nabla \psi \right) \cdot \hat n dS$$
Then, using Stokes Theorem, integrating both sides over the surface S, and swapping the LHS for the line integral and using the scalar triple product identity for the RHS:
$$\left( - \vec B \times \nabla \psi \right) \cdot \hat n dS = \left(\nabla \psi \times \vec B \right) \cdot \hat n dS = \left(\hat n \times \nabla \psi \right) \cdot \vec B dS$$
$$\oint \left( \psi \vec B \right) \cdot d\vec r = \iint_S \left(\hat n \times \nabla \psi \right) \cdot \vec B dS$$

What I have there doesn't look too different from the required solution, however I believe that I may have made a grave error along the way. Would anyone be able to provide me with some suggestions/hints on how to proceed?

Thanks in advance

 

[Infrared]

You can re-write your last line as $B\cdot \left(\oint_C \psi \ dr\right)=B\cdot\left(\iint_S (\hat{n}\times\nabla\psi) dS\right)$. In general if $v$ and $w$ are vectors and $B\cdot v=B\cdot w$ for all vectors $B$, then $v$ must equal $w$.

 

[Master1022]

You can re-write your last line as $B\cdot \left(\oint_C \psi \ dr\right)=B\cdot\left(\iint_S (\hat{n}\times\nabla\psi) dS\right)$. In general if $v$ and $w$ are vectors and $B\cdot v=B\cdot w$ for all vectors $B$, then $v$ must equal $w$.

Many thanks. Yes, that makes sense.