Help Finding Amplitude of Voltage Across Capacitor At Resonant Frequency

[mmmboh]

Hi, here is the question:

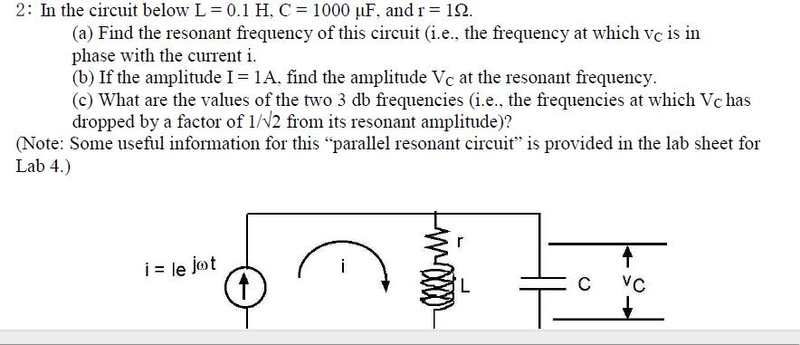
For part b) I have to find the amplitude of V_c at the resonant frequency with I=1A, I have found Z_eq and well here are my equations:

$$\frac{jwL+R}{\ jwRC-w^2LC+1}$$ and I have the equation for w at the resonance:w= $$\sqrt[2]{\frac{L-R^2C}{\L^2C}}$$

I know at the resonant the impedance is real..but I don't know what to do with my equations, can someone help please.

 

[ehild]

Multiply both the numerator and the denominator of the impedance by the complex conjugate of the denominator. That makes the denominator real. Then it is easy to find the condition for real impedance: when the imaginary part of the numerator is zero.

ehild

 

[mmmboh]

Oh I figured it out...thanks!