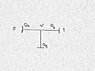Archived Help finding Effective Capacitance in a Circuit

[nishantve1]

Homework Statement

The Question is to find Effective capacitance in the circuit shown below (Sorry if the pic is not clear enough)

Homework Equations

This is in the Chapter Capacitors so the basic formula that would be used I guess is Q = CV

The Attempt at a Solution

First I Identified the Points with uniform Potentials and Named them ABCD
A and B being the extremes
then I connected a battery mentally between points A and B
then I induced the charges
{its hard to show without the picture but I hope it makes sense }

then I used the Formula Q = CV

I have solved simpler circuits using simple formulas like this one I mean just this but I was wondering if there was any kind of tricks to easily solve these , I have heard of Star Delta Conversion will that be applicable in this or Loop method IDK . Or should I move ahead to the next Chapters Resistors and Current and then try to solve these
Please help
Thanks

 

[gneill]

You can do mesh analysis or nodal analysis on a system where charge has flowed to form a static arrangement of potential differences. Rather than working with potential drops that are due to a flowing current we work with the static potentials that result from some total charges that have moved into place.

Let's try nodal analysis. Suppose there's a capacitor situated between two nodes A and B with assumed potentials VA and VB. Then the potential difference across that capacitor from A to B is (VA - VB). In order to have that potential difference, some charge q = (VA - VB)C must have flowed out of node A and into the capacitor, and from the capacitor to node B, leaving the capacitor charged to that potential difference. We can write such terms for every essential node in the circuit.

For the circuit in this problem there are four essential nodes if we pick one node as a reference node. It's convenient to choose the reference node to be one of the terminals, and to inject some fixed charge Q into the other terminal.

All capacitance values are assumed to be in μF. Writing node equations:

Node v1: $~~-Q + (v1 - v2)1 + (v1 - v3)2 + (v1 - v4)3 = 0$

Node v2: $~~(v2 - v1)1 + (v2 - v3)4 + (v2)3 = 0$

Node v3: $~~(v3 - v1)2 + (v3 - v2)4 + (v3 - v4)4 + (v3)2 = 0$

Node v4: $~~(v4 - v1)3 + (v4 - v4)4 + (v4)1 = 0$

The above equations can be solved fairly easily. The only value we need is v1, since it represents the potential across the equivalent capacitance (it's the potential between the terminals of the circuit). Then $C_{eqiv} = Q/v1$.

Solving for v1 yields: $v1 = \frac{4}{11}Q$. That makes the equivalent capacitance $C_{equiv} = \frac{11}{4}~μC$.

 

[epenguin]

Quite devilish - the books and online sources deal monotonously with circuited easily broken up into 'series' and 'parallel' bits, but connections here are not that simple.

I have noticed in recent problems like this about capacitor or resistance networks, that their calculation could often be drastically simplified because they had symmetries in them. I don't know whether this is to simplify for the people who set them and they want you to work them out longwindedly, as you have to be able to know how to do, or whether they want you to notice and use the symmetries. Also I notice that excercises and book or online explanations are very much formula application, with physical insights not so stressed.

There seems no way I can tell you this by hints, so except for potential signs, this circuit is the same when you rotate it through 180°
Let the applied potential be 1 V, I will just say 1 sometimes without the units. Working out equivalent capacitances is working out overall charges, but we have to get individual ones to get there probably.Let me represent the capacitors in your circuit as
a. b
c. d
e. f. for the horizontal branches and

g
h. for the vertical ones.

By the symmetry the potential at the centre point can only be ½.
So we easily work out the charges on c and d, they are each ½×2 = 1 μC.

The potential at the centre would be still be ½ if we removed c and d. (And it would be ½ if we removed everything except c and d.) So we can just note the above charges to bring back later, but all other charges and potentials are the same if c and d are not there. So we sort out a simplified circuit with these absent. We can if we wish then condense g and h into a single 2μF capacitor.

At which point I am getting late-night fallible. Certainly if we assigned a potential, V' say, to the bottom midpoint, that at the top is (1 - V') and we have a considerably simplified calculation. But it seems to me that this V' too should be ½ ! (And so V' = (1 - V') ). That the 'vertical' capacitor(s) are uncharged. Only that way can all the capacitors be overall neutral, the positive charge facing an equal negative charge on a facing plate. (And btw wouldn't that apply aLao in cases without symmetry?)

Then g and h can be removed from the calculation and we are left with a very simple circuit, two parallel capacitors which we can put in parallel with the 1 μC, i.e. 1 μF one we had above. I am getting 2½ μF, not quite gneill's, but it is late at night. More complete standard methods calculating should be done especially to check the reasoning of the previous para, for if intuition can guide and shorten calculations, calculation can educate intuition.

Whenever you have symmetry think to use it anyway.

 

[cnh1995]

Three star delta conversions will give the answer. But for capacitors, equations are different.

 

[epenguin]

Yeah I think the part I wrote yesterday night and have now crossed through is wrong. But the rest stands.

Possibly the easiest way to do the second part of the calculation is not to combine g and h but to calculate the charges in the T consisting of the branches a, b, g where we know the potentials terminals of the T, namely 0, 1 and ½ (and we will have the same potentials and charges in the other T consisting of branches f, e,h).

 

[epenguin]

Now done this by the method I indicated, which is very simple calculation, and got the same answer as gneiss. However we haven't heard further from the OP.

 

[gneill]

However we haven't heard further from the OP.

And we very likely won't. The post is from 2012. That is why it's been moved to this forum, where complete solutions are permitted.

 

[epenguin]

OK, I had just seen this question among the new ones without noticing it was old and had been bumped for some reason.

In couple of previous posts I was pointing out how symmetry allowed simplification from the start in the analysis of some resistive networks.
How to find the equivalent resistance?
How to calculate the equivalent resistance using wye delta ?
It allowed disconnection at some junctions without altering current flows. Here it allows some disconnection without changing charges or potentials.

For easy calculation I will just take the potential difference across the circuit to be 1 V; then the equivalent capacitance is the same as charge on the terminal plates.

This circuit is unchanged (except for polarity, irrelevant to equivalent capacitance) when it is rotated through 180°.

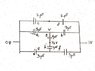
Then by symmetry the potential at the central point of the OP's diagram (v₃ in gniell's ) must be ½ V. The potential there will still be this if the branches of the 'middle vertical' (I called these g and h) are disconnected from the 'middle horizontal' (branches c,d). So disconnecting in this way the circuit is equivalent to (attachment 1)

The equivalent capacitance of the top branch is 1μF.

All the rest of the circuit is in parallel with it. I find it convenient now to not condense g and h. Instead consider just the charges on the plates of a, b and g - if we consider them with signs, as the total charge of this T structure, conductively isolated (see attachment 2), must add up to 0.i.e. Q_a + Q_b + Q_g = 0.

Using the capacitance law (or definition some might prefer)

Q_a= v, Q_b = 3(v - 1), Q_g = 4(v - ½)

Substituting the second set in the first equation gives

v + 3(v -1) + 4(v - ½) = 8v - 5 = 0

and so v = 5/8.

Hence again by the capacitance laws , Q_a =3/8, Q_b = -9/8

By the symmetry the charge on the plate at f is the same (in magnitude) as that on a , i.e. 5/8, or with sign -5/8.

The total negative charge on the plates opposite to the plates held at 1V, and hence the equivalent capacitance, is thus

|Q_b + Q_f + Q_d| = 9/8 + 3/8 + 1 = 11/4, in agreement with gniell.

An easier calculation than it seemed this was going to be at first sight (though I would like to improve the formulation around the issue of charge signs).