moshiko
- 2
- 0
Hello everyone,
Looking for a more efficient solution to method 'what', in terms of run-time complexity and space.
The method finds the largest cell sequence that the organs sum is divided by 3.(Correct me if I'm wrong)
As it seems runtime complexity here is O(n ^ 3).
I came to solution of O(n ^ 2), is there a more effective solution? Explain please,
Thanks for the helpers !
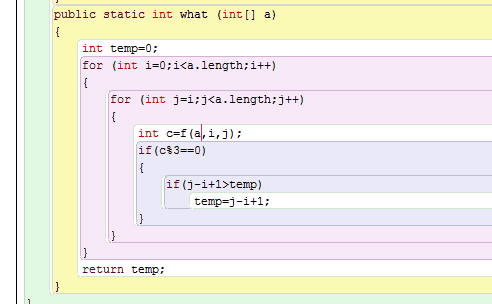
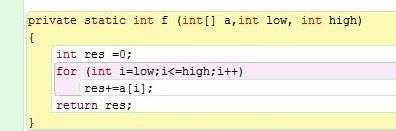
Looking for a more efficient solution to method 'what', in terms of run-time complexity and space.
The method finds the largest cell sequence that the organs sum is divided by 3.(Correct me if I'm wrong)
As it seems runtime complexity here is O(n ^ 3).
I came to solution of O(n ^ 2), is there a more effective solution? Explain please,
Thanks for the helpers !