lorenz0
- 151
- 28
- Homework Statement
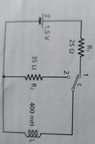
- At the beginning the switch c of the circuit is in position 1. At t=0, it switches to position 2.
(1) Find ##I(0).## (2) Find ##t*## such that ##I(t*)=35mA.##
- Relevant Equations
- ##I(t)=I(0)(1-e^{(-R/L)t)},\ I(0)=\frac{V}{R}##
What I have done:
(1) ##I(0)=\frac{V}{R}=\frac{1.5}{25}A=0.06 A.##
(2) By setting ##I(t*)=0.06(1-e^{-(35/0.4)t*})=35 mA## we get ##t*\approx 0.01 s##
What I have done seems correct to me, but the result for part (2) should be different.
I would be grateful if someone could point out to me where I have made a mistake.
(1) ##I(0)=\frac{V}{R}=\frac{1.5}{25}A=0.06 A.##
(2) By setting ##I(t*)=0.06(1-e^{-(35/0.4)t*})=35 mA## we get ##t*\approx 0.01 s##
What I have done seems correct to me, but the result for part (2) should be different.
I would be grateful if someone could point out to me where I have made a mistake.
Attachments
Last edited: