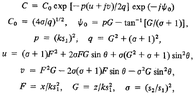Bart Bas
- 1
- 1
- TL;DR
- I need help with a derivation of an equation given in a journal paper. Although it is about fibre coupling my problem is purely mathematical. It is about solving a complex double integral.
I need help with a derivation of an equation given in a journal paper. My question is related to the third paragraph of this paper: https://doi.org/10.1007/BF00619826. Although it is about fibre coupling my problem is purely mathematical. It is about solving a complex double integral. The information that I give below should be enough to understand the problem so access to the paper is not necessary.
My problem can be narrowed down to solving the equation $$C=\frac{\sqrt{n_1}}{2Z_0P} \int_0^\infty \int_0^{2\pi} E_\xi {E_{\xi^\prime}}^* \rho^\prime d\rho^\prime d\phi^\prime.$$ Substituting the right equations for ##E_\xi## and ##E_{\xi^\prime}## gives $$C=\frac{\sqrt{n_1}}{2Z_0P} \int_0^\infty \int_0^{2\pi} \sqrt{\frac{2Z_0P}{\pi w^2}} \exp\left(-\frac{1}{2 w^2}\rho^2\right) \exp\left(-j\frac{k}{2R}\rho^2\right) \exp\left(-jk\zeta\right) \exp\left(j \arctan\left(\frac{z}{k{s_1}^2}\right)\right) {\left(\sqrt{\frac{2Z_0P}{\pi n_1{s_2}^2}} \exp\left(-\frac{{\left(\rho^\prime/s_2\right)}^2}{2}\right) \right)}^* \rho^\prime d\rho^\prime d\phi^\prime.$$ Simplifying a little gives $$C=\frac{1}{\pi w s_2} \int_0^\infty \int_0^{2\pi} \exp\left(-\frac{1}{2 w^2}\rho^2\right) \exp\left(-j\frac{k}{2R}\rho^2\right) \exp\left(-jk\zeta\right) \exp\left(j \arctan\left(\frac{z}{k{s_1}^2}\right)\right) \exp\left(-\frac{{\left(\rho^\prime/s_2\right)}^2}{2}\right) \rho^\prime d\rho^\prime d\phi^\prime.$$
The variables ##\rho## and ##\zeta## still need to be expressed in terms of the variables of integration using the equations $$\rho^2 \simeq {\left(\rho^\prime\right)}^2 + 2\rho^\prime x \cos\left(\phi^\prime\right) + x^2 $$ and $$\zeta = \rho^\prime \cos\left(\phi^\prime\right) \sin\left(\theta\right) + z.$$ Furthermore, ##j## represents the imaginary unit. The variables ##k##, ##s_1##, and ##s_2## are positive real numbers. The variables ##x##, ##z##, and ##\theta## are real numbers. Finally the parameters ##w## and ##R## are given by $$w=s_1 \sqrt{1 + {\left(\frac{z}{k{s_1}^2}\right)}^2}$$ and $$R=z\left(1+{\left(\frac{k{s_1}^2}{z}\right)}^2\right).$$
Only accompanied by the text "after lengthy manipulations we obtain" the paper presents the results of carrying out the integral as given in an attachment to this post. The only hint that I did not already use in simplifying my question here is a footnote from the paper which I also attached to this post. I have not been able to find a way to come to this result or see when to use the formula in the footnote.
Evaluating the inner integral first would in its most basic form result into something like $$\int_0^{2\pi} \exp\left(a \cos\left(\phi^\prime\right)\right) d\phi^\prime = 2 \pi \operatorname{I_0}\left(a\right).$$ Here I assumed that all terms that do not depent on ##\phi^\prime## are taken outside the integral. This unfortunatley is only valid if ##a## would be real, however, because ##a## is a combination of all other terms it is complex valued. I am not sure if there even exists a solution when ##a## is complex. Evaluating the outer integral first would in its most basic form result into something like $$\int_0^\infty \rho^\prime \exp\left(b{\left(\rho^\prime\right)}^2+c\rho^\prime\right) d\rho^\prime = \frac{-2b+c\sqrt{-b}\exp\left(-\frac{c^2}{4b}\right)\sqrt{\pi}\operatorname{Erfc\left(-\frac{c}{2\sqrt{-b}}\right)}}{4b^2}.$$ Again ##b## and ##c## are complex valued.
I do not see how this can lead to the result as presented in the paper. I think I overlook a possible simplification before carrying out the integral. I did spend quite some days on it trying it by hand with the help of Wolfram Alpha. I also tried to learn Mathematica and use that to solve the entire equation at once, but this was no success either.
I tried to keep the problem concise by giving just enough information and not blurring you with the details. In case I missed something or something needs clarifying please let me know! Any help or push in the right direction would be highly appreciated!
Regards, Bart.
My problem can be narrowed down to solving the equation $$C=\frac{\sqrt{n_1}}{2Z_0P} \int_0^\infty \int_0^{2\pi} E_\xi {E_{\xi^\prime}}^* \rho^\prime d\rho^\prime d\phi^\prime.$$ Substituting the right equations for ##E_\xi## and ##E_{\xi^\prime}## gives $$C=\frac{\sqrt{n_1}}{2Z_0P} \int_0^\infty \int_0^{2\pi} \sqrt{\frac{2Z_0P}{\pi w^2}} \exp\left(-\frac{1}{2 w^2}\rho^2\right) \exp\left(-j\frac{k}{2R}\rho^2\right) \exp\left(-jk\zeta\right) \exp\left(j \arctan\left(\frac{z}{k{s_1}^2}\right)\right) {\left(\sqrt{\frac{2Z_0P}{\pi n_1{s_2}^2}} \exp\left(-\frac{{\left(\rho^\prime/s_2\right)}^2}{2}\right) \right)}^* \rho^\prime d\rho^\prime d\phi^\prime.$$ Simplifying a little gives $$C=\frac{1}{\pi w s_2} \int_0^\infty \int_0^{2\pi} \exp\left(-\frac{1}{2 w^2}\rho^2\right) \exp\left(-j\frac{k}{2R}\rho^2\right) \exp\left(-jk\zeta\right) \exp\left(j \arctan\left(\frac{z}{k{s_1}^2}\right)\right) \exp\left(-\frac{{\left(\rho^\prime/s_2\right)}^2}{2}\right) \rho^\prime d\rho^\prime d\phi^\prime.$$
The variables ##\rho## and ##\zeta## still need to be expressed in terms of the variables of integration using the equations $$\rho^2 \simeq {\left(\rho^\prime\right)}^2 + 2\rho^\prime x \cos\left(\phi^\prime\right) + x^2 $$ and $$\zeta = \rho^\prime \cos\left(\phi^\prime\right) \sin\left(\theta\right) + z.$$ Furthermore, ##j## represents the imaginary unit. The variables ##k##, ##s_1##, and ##s_2## are positive real numbers. The variables ##x##, ##z##, and ##\theta## are real numbers. Finally the parameters ##w## and ##R## are given by $$w=s_1 \sqrt{1 + {\left(\frac{z}{k{s_1}^2}\right)}^2}$$ and $$R=z\left(1+{\left(\frac{k{s_1}^2}{z}\right)}^2\right).$$
Only accompanied by the text "after lengthy manipulations we obtain" the paper presents the results of carrying out the integral as given in an attachment to this post. The only hint that I did not already use in simplifying my question here is a footnote from the paper which I also attached to this post. I have not been able to find a way to come to this result or see when to use the formula in the footnote.
Evaluating the inner integral first would in its most basic form result into something like $$\int_0^{2\pi} \exp\left(a \cos\left(\phi^\prime\right)\right) d\phi^\prime = 2 \pi \operatorname{I_0}\left(a\right).$$ Here I assumed that all terms that do not depent on ##\phi^\prime## are taken outside the integral. This unfortunatley is only valid if ##a## would be real, however, because ##a## is a combination of all other terms it is complex valued. I am not sure if there even exists a solution when ##a## is complex. Evaluating the outer integral first would in its most basic form result into something like $$\int_0^\infty \rho^\prime \exp\left(b{\left(\rho^\prime\right)}^2+c\rho^\prime\right) d\rho^\prime = \frac{-2b+c\sqrt{-b}\exp\left(-\frac{c^2}{4b}\right)\sqrt{\pi}\operatorname{Erfc\left(-\frac{c}{2\sqrt{-b}}\right)}}{4b^2}.$$ Again ##b## and ##c## are complex valued.
I do not see how this can lead to the result as presented in the paper. I think I overlook a possible simplification before carrying out the integral. I did spend quite some days on it trying it by hand with the help of Wolfram Alpha. I also tried to learn Mathematica and use that to solve the entire equation at once, but this was no success either.
I tried to keep the problem concise by giving just enough information and not blurring you with the details. In case I missed something or something needs clarifying please let me know! Any help or push in the right direction would be highly appreciated!
Regards, Bart.