Help Needed with Determining B' in Proposition 6.1.2: A Case for n=2

[Math Amateur]

(Note: I have posted a similar post to this recently, but have had no replies ... I am now posting a similar but simple and more focused post with less scope)
I am reading Multidimensional Real Analysis II (Integration) by J.J. Duistermaat and J.A.C. Kolk ... and am focused on Chapter 6: Integration ...

I need some help with the proof of Proposition 6.1.2 ... and for this post I will focus on the first auxiliary result ... see (i) ... at the start of the proof ...

Proposition 6.1.2 ... and the start of the proof ... reads as follows:

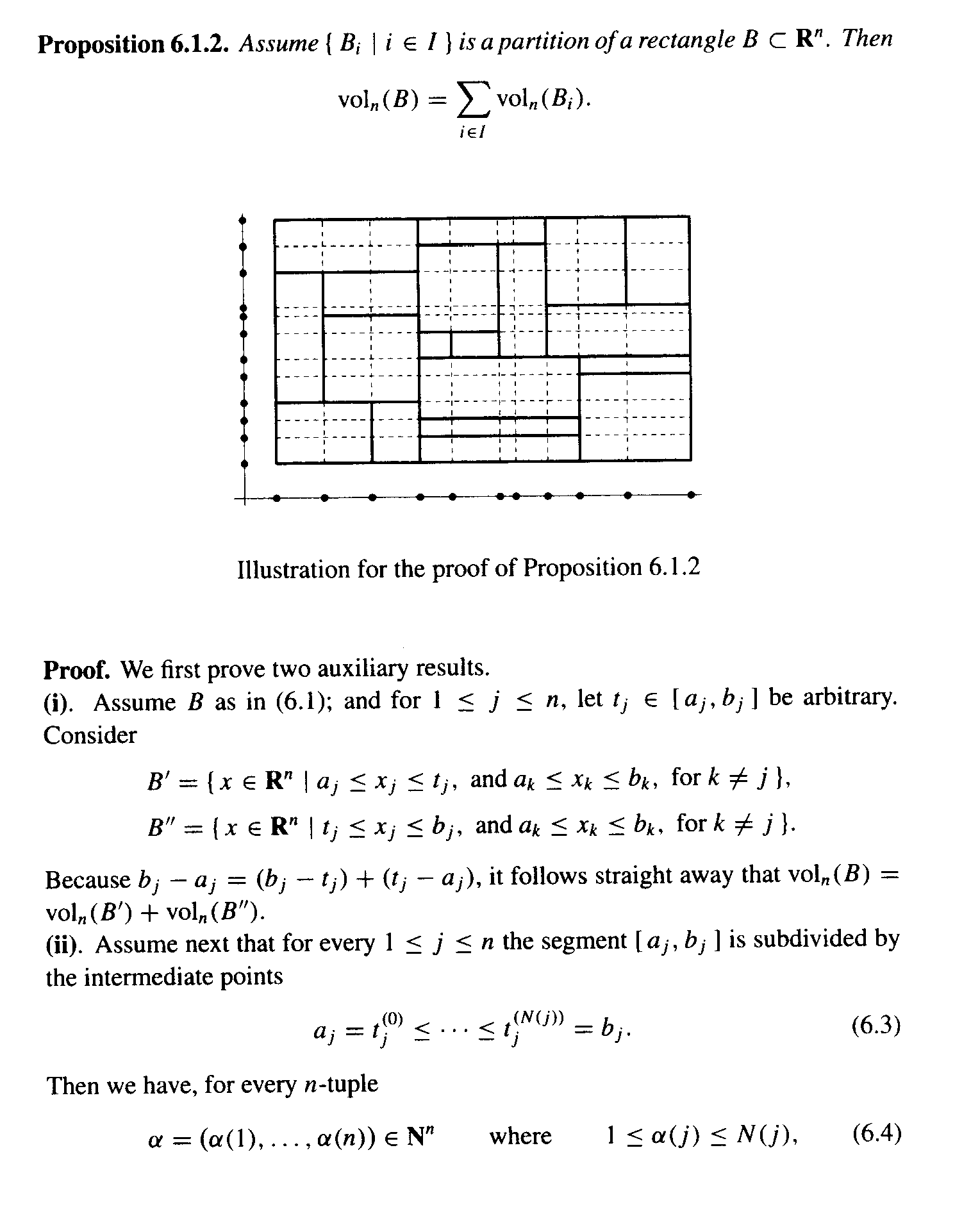
Definitions and text preliminary to the Proposition reads as follows:

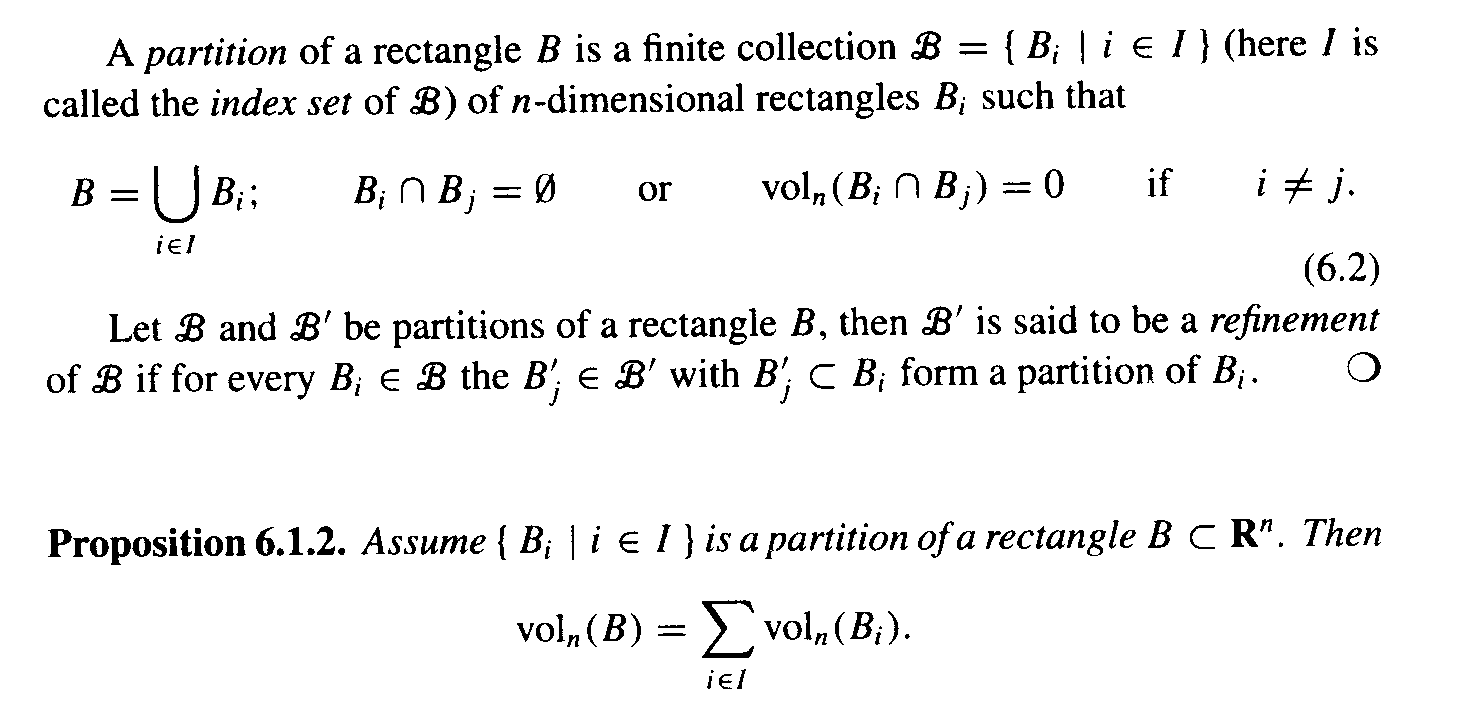At the start of the proof in (i) D&K write :

" ... for [math] 1 \leq j \leq n, \text{ let } t_j \in [a_j, b_j] [/math] be arbitrary.

Consider

[math] B' = \{ x \in \mathbb{R^n} \ \ | \ \ a_j \leq x_j \leq t_j \text{ and } a_k \leq x_k \leq b_k \text{ for } k \neq j \} [/math]

... now ... to simplify the situation ... consider the case for [math] n = 2 [/math] ... that is for math] R^2 [/math] ...

Thus we consider :

[math] B' = \{ ( x_1, x_2 ) \in \mathbb{R^2} \ \ | \ \ a_j \leq x_j \leq t_j \text{ and } a_k \leq x_k \leq b_k \text{ for } k \neq j \} [/math]

where [math] 1 \leq j \leq 2 [/math]*** Now my problem is how do we validly and correctly determine B' ... ***

The sets involved in determining B' are as follows:

For $ j=1$ we consider the set : $ a_1 \leq x_1\leq t_1 \text{ and } a_2 \leq x_2 \leq b_2 $

For $ j=2 $ we consider the set : $ a_2 \leq x_2 \leq t_2 \text{ and } a_1 \leq x_1 \leq b_1$Now ... with these sets ... do we :

$ \bullet $ Take $j=1$ or take $j=2 $ and just consider one set

$ \bullet $ Consider the case for $j=1$ or $j=2$ ... that is , take the union of both sets

$ \bullet $ Consider the case for $j=1$ and $j=2$ ... that is , take the intersection of both setsI think the correct option is to take the intersection of both sets since in the initial specification of B' both conditions seem to apply ...Is that correct?

If it is not correct can someone please explain the mistakes, shortcomings and deficiencies ...
If the intersection is the valid and correct way to proceed then :

[math] B' = \{ ( x_1, x_2 ) \in \mathbb{R^2} \ \ | \ \ a_1 \leq x_1 \leq t_1 \text{ and } a_2 \leq x_2 \leq t_2 \} [/math]Is that correct?Hoping someone can help .

... any help will be much appreciated ...

Peter

 

[GJA]

Hi Peter,

Great job looking to $\mathbb{R}^{2}$ to gain an intuition for what's going on. Also really nice that you've posited a number of possible interpretations of what the author has written. You've done a great job outlining testable criteria, so let's do just that.

Suppose the author meant to look at the intersection. Take $B = [0,1]\times [0,1]$; i.e., $B$ is the unit square in $\mathbb{R}^{2}$. Take $t_{1} = 0.25$ and $t_{2} = 0.75$. Then, under the intersection interpretation, $B'$ is shown in green below and $B''$ is shown in red below. We can see that $\text{Vol}_{2}(B)\neq \text{Vol}_{2}(B') + \text{Vol}_{2}(B'')$ because the right side of the equation is smaller than the quantity on the left.

I encourage you to try using the same example under the "union interpretation." In this case you will get "L"-shaped regions for $B'$ and $B''$, and $\text{Vol}_{2}(B') + \text{Vol}_{2}(B'')$ will exceed $\text{Vol}_{2}(B).$

I believe the author's intention here is to fix a value of $j$ between 1 and $n$. Then, for this $j$ pick $t_{j}$ arbitrarily. The equality will then hold and this is true for any $j$ we could choose. The picture of this for $j=1$ on the unit square is shown below and we can see that equality does hold. See second picture with orange and blue regions.

[DESMOS]{"version":7,"graph":{"viewport":{"xmin":-0.1,"ymin":-0.1,"xmax":1.25,"ymax":1.25},"squareAxes":false},"randomSeed":"1e19c72bef2e1f81b4bc890d13ccd9f9","expressions":{"list":[{"type":"expression","id":"1","color":"#388c46","latex":"0\\le y\\le0.75\\left\\{0\\le x\\le0.25\\right\\}"},{"type":"expression","id":"2","color":"#eb4034","latex":"0.75\\le y\\le1\\left\\{0.25\\le x\\le1\\right\\}"}]}}[/DESMOS]

[DESMOS]{"version":7,"graph":{"viewport":{"xmin":-0.1,"ymin":-0.1,"xmax":1.25,"ymax":1.25},"squareAxes":false},"randomSeed":"744dbacbbd651d06cd2e923a05d09284","expressions":{"list":[{"type":"expression","id":"1","color":"#fa7e19","latex":"0\\le y\\le1\\left\\{0\\le x\\le0.75\\right\\}"},{"type":"expression","id":"2","color":"#2d70b3","latex":"0\\le y\\le1\\left\\{0.75\\le x\\le1\\right\\}"}]}}[/DESMOS]

 

[Math Amateur]

Hi Peter,

Great job looking to $\mathbb{R}^{2}$ to gain an intuition for what's going on. Also really nice that you've posited a number of possible interpretations of what the author has written. You've done a great job outlining testable criteria, so let's do just that.

Suppose the author meant to look at the intersection. Take $B = [0,1]\times [0,1]$; i.e., $B$ is the unit square in $\mathbb{R}^{2}$. Take $t_{1} = 0.25$ and $t_{2} = 0.75$. Then, under the intersection interpretation, $B'$ is shown in green below and $B''$ is shown in red below. We can see that $\text{Vol}_{2}(B)\neq \text{Vol}_{2}(B') + \text{Vol}_{2}(B'')$ because the right side of the equation is smaller than the quantity on the left.

I encourage you to try using the same example under the "union interpretation." In this case you will get "L"-shaped regions for $B'$ and $B''$, and $\text{Vol}_{2}(B') + \text{Vol}_{2}(B'')$ will exceed $\text{Vol}_{2}(B).$

I believe the author's intention here is to fix a value of $j$ between 1 and $n$. Then, for this $j$ pick $t_{j}$ arbitrarily. The equality will then hold and this is true for any $j$ we could choose. The picture of this for $j=1$ on the unit square is shown below and we can see that equality does hold. See second picture with orange and blue regions.

[DESMOS]{"version":7,"graph":{"viewport":{"xmin":-0.1,"ymin":-0.1,"xmax":1.25,"ymax":1.25},"squareAxes":false},"randomSeed":"1e19c72bef2e1f81b4bc890d13ccd9f9","expressions":{"list":[{"type":"expression","id":"1","color":"#388c46","latex":"0\\le y\\le0.75\\left\\{0\\le x\\le0.25\\right\\}"},{"type":"expression","id":"2","color":"#eb4034","latex":"0.75\\le y\\le1\\left\\{0.25\\le x\\le1\\right\\}"}]}}[/DESMOS]

[DESMOS]{"version":7,"graph":{"viewport":{"xmin":-0.1,"ymin":-0.1,"xmax":1.25,"ymax":1.25},"squareAxes":false},"randomSeed":"744dbacbbd651d06cd2e923a05d09284","expressions":{"list":[{"type":"expression","id":"1","color":"#fa7e19","latex":"0\\le y\\le1\\left\\{0\\le x\\le0.75\\right\\}"},{"type":"expression","id":"2","color":"#2d70b3","latex":"0\\le y\\le1\\left\\{0.75\\le x\\le1\\right\\}"}]}}[/DESMOS]

Hi GJA,

I've read through your post a number of tiimes ...

Thanks for such a helpful and detailed post that is also quite motivating and interesting ...

Thanks again ...

Peter

 

[Opalg]

Hi Peter! It's good to see you back here after a long break.

GJA has answered your questions much better than I could, so I won't try to say much more. Just to reiterate: the key point is that the index $j$ is fixed, in the definitions of the sets $B'$ and $B''$. The idea is that you slice through the $j$th coordinate of the set $B$. In the case of GJA's orange and blue diagram, the $j$th coordinate is the $x$-coordinate, and the unit square is sliced through by the vertical line $x= 0.75$. Notice that the orange and blue sets form a partition of the unit square. They are not disjoint because they have a nonempty intersection, namely the line segment $\{(x,y) : x=0.75,\ 0\leqslant y\leqslant 1\}$. But that line segment has zero 2-dimensional volume, so Duistermaat and Kolk's definition of partition is satisfied.

 

[Math Amateur]

Thanks for a helpful post ... and a big thank you to you and GJA for all your help in the past ...

Especially helpful was the note about the non-empty intersection ... D&K mentioned intersections of zero volume and i wondered what they were referring to ... understand now ...

Absence was due to some health issues which are now being managed ...

Thanks again ...

Peter