Solve First Order Homogeneous ODE | Constants a and b | Help Needed!

[Konig]

Hi, need help solving a first order homogeneous ODE.

y'(x)-(a/x)y = b/(x(1+x)^2) Here a and b are some constants.

Need to solve this for y.

My attempts so far have been to use

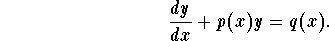
But this means solving ∫ x^(-a)/(x(1+x)^2) dx which has solutions in terms of Gauss hyper-geometric functions,

http://en.wikipedia.org/wiki/Hypergeometric_function"

Which lead me to believe I'm going wrong somewhere...

Sorry for the maths format, I'm new to here and don't know how to insert LaTeX.

Thanks

 

[jackmell]

What, he didn't give you an easy one huh? But isn't the integrating factor x^(-a) so that you get:

d(yx^{-a})=\frac{b}{x^{1+a}(1-x)^2}

Now suppose all you had to do was:

\int \frac{b}{x^{1+a}(1-x)^2}dx

Could you use parts say, one, two, three, four times, look at what's happening to the sequence, then come up with a general (infinite-term) expression for the solution that when you checked out the power-series expression for the Hypergeometric series solution reported by Mathematica, the series you get looks like it?

 

[Konig]

thanks for the response Jackmell,

Am currently working on it, though keep making maths errors which are slowing me down.

I agree it would be a good idea to compare, thanks for the tip.

The problem is part of a project, so yea the problems not meant to be easy.
demoralising thing though is that I'm not sure i was supposed to take this long with it!

Konig