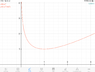
Help solving this equation please: y^2-2ln(y)=x^2

[majdgh]

Homework Statement

Solving equation

Relevant Equations

y^2-2ln(y)=x^2

Hello,
Please can someone help me to solve this equation:
y^2-2ln(y)=x^2
I want to find y =?
Thanks in advance.

 

[berkeman]

Homework Statement:: Solving equation
Relevant Equations:: y^2-2ln(y)=x^2

Hello,
Please can someone help me to solve this equation:
y^2-2ln(y)=x^2
I want to find y =?
Thanks in advance.

Welcome to the PF.

We require that you show your best efforts to solve this problem before we can offer tutorial help. What ideas do you have so far on how to approach this problem? What section of your textbook is this problem from?

$y^2-2ln(y)=x^2$

 

[majdgh]

Hello
You can see the picture, but I got stucked, I wanted to find y

 

[haruspex]

Homework Statement:: Solving equation
Relevant Equations:: y^2-2ln(y)=x^2

Hello,
Please can someone help me to solve this equation:
y^2-2ln(y)=x^2
I want to find y =?
Thanks in advance.

Pretty sure there is no closed form solution, but there are a couple of things you can do.

First, the equation can be simplified somewhat by substituting other variables for x and y, X and Y say. Can you see how a substitution for y simplifies both terms it occurs in?

Having done that, you could write a sequence of approximations for Y in terms of X, giving Y as an infinite sequence of functions of X.

 

[scottdave]

When looking for ways to simplify it, think about what multiplying or adding logarithms do.

 

[William Crawford]

It is possible to express $y$ in terms of $x$. From your calculations you have that
$$y^{-2}e^{y^2} = e^{x^2},$$
this it great. Rearrange the equation to look like
$$-y^2e^{-y^2} = -e^{-x^2}.$$
This is an equation of the form $we^w = z$ and can thus be solved using the Lambert $W$ function <LINK>. Accordingly
$$-y^2 = W_0\big(-e^{-x^2}\big) \qquad\vee\qquad -y^2 = W_{-1}\big(-e^{-x^2}\big),$$
provided that $\vert x\vert\geq1$. Finally, note that both $W_{-1}$ and $W_0$ are negative valued for $\vert x\vert\geq1$. Thus
$$ y = \pm\sqrt{-W_{k}\big(-e^{-x^2}\big)},\quad k =-1,0\ \text{and}\ \vert x\vert\geq1.$$

UPDATE
Thought I would include a plot of the solution as well.

The red curve corresponds to the solution $y = \sqrt{-W_{-1}\big(-e^{-x^2}\big)}$.
The green curve corresponds to the solution $y = -\sqrt{-W_{-1}\big(-e^{-x^2}\big)}$.
The blue curve corresponds to the solution $y = \sqrt{-W_{0}\big(-e^{-x^2}\big)}$.
The magenta curve corresponds to the solution $y = -\sqrt{-W_{0}\big(-e^{-x^2}\big)}$.

 

[haruspex]

can thus be solved using the Lambert W function

... though whether it constitutes a closed form solution is a matter of taste.

 

[William Crawford]

... though whether it constitutes a closed form solution is a matter of taste.

I agree.

 

[epenguin]

Yeah I was going to say.
What we have here is, let's say, a relation between $x$ and $y$. We can write that $y=f(x)$ . By definition then $x=f^{-1}\left( y\right)$ and we call $f^{-1}$ the inverse of $f$. We are used to plotting $x$ against $y$; given $x$ we can then read off $y$. But just as easily, given $y$ we can read $x$ off the same graph.

What happens is that years of school etc training tend to brainwash us into the habit of explicitly calculating the inverse function, i.e. given $y$ calculate $x$, I.e. invert the function. which might be a logical thing to do in some cases but not in the following:

when there is no way to do it, i.e. no known inverse function;
when there might be a way to do it but you don't know what it is and it would be long to find out;
when there is a way of doing it, but it is so complicated that is not worth it; when the formula for the solution so to say does not speak to you, the way that simple enough formulae do.

If the problem is knowing $y$ find $x$, graphically this is nothing new as explained above. Numerically, many scientific calculators or function plotters have routines which if you can calculate any function, can calculate its inverse to all accuracy you are likely to need.

In the present case we could say we have a relationship between two variables we can call $x^{2}$ and $y^{2}$. $x^{2}$ ≥ 0 but $y^{2}$≥ 1. To every value of $x^{2}$ corresponds one value of $y^{2}$, but to every value of $y^{2}$ corresponds two of $x^{2}$, see fig 1. Simples.

If we want it as function of $x$ itself see fig 2.

So a qualitative answer to the question is that to every y ≥ 1 corresponds four values of x in the form ± x₁, ± x₂
At risk of belaboring the obvious, when you have Y=X² and you write X= ±√Y and say you have solved something, you haven't, you haven't done anything except show you know the special symbol for the inverse of squaring. The mathematical substance lies in the fact you know how to calculate that. Don't you?

This Lambert function does come up in some applications e.g. in enzyme kinetics, so it is good to know about the implementation mentioned by W Crawford.

For negative $y$ most of us might not want to get into $ln$ of negative numbers so I think that those two figs. sufficient.