- #1
Help solving this equation please: y^2-2ln(y)=x^2
- Thread starter majdgh
- Start date
Click For Summary
SUMMARY
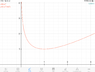
The equation y2 - 2ln(y) = x2 does not have a closed-form solution. Instead, it can be approached using the Lambert W function, which allows for expressing y in terms of x as y = ±√(-Wk(-e-x2)), where k can be -1 or 0, applicable for |x| ≥ 1. The discussion emphasizes the relationship between x and y, illustrating that for every y ≥ 1, there are four corresponding x values. Graphical representations of the solutions are also provided, showcasing the behavior of the functions involved.
PREREQUISITES- Understanding of logarithmic functions, specifically natural logarithms (ln)
- Familiarity with the Lambert W function and its applications
- Basic knowledge of algebraic manipulation and function inversion
- Graphing skills to visualize relationships between variables
- Study the properties and applications of the Lambert W function
- Learn about numerical methods for solving equations without closed forms
- Explore graphical methods for analyzing relationships between variables
- Investigate the implications of the Lambert W function in fields like enzyme kinetics
Mathematicians, students tackling advanced algebra, researchers in fields utilizing the Lambert W function, and anyone interested in solving complex equations involving logarithmic and polynomial relationships.
- #2
berkeman
Admin
- 69,341
- 24,655
Welcome to the PF.majdgh said:
We require that you show your best efforts to solve this problem before we can offer tutorial help. What ideas do you have so far on how to approach this problem? What section of your textbook is this problem from?
##y^2-2ln(y)=x^2##
- #3
- #4
- 42,802
- 10,495
Pretty sure there is no closed form solution, but there are a couple of things you can do.majdgh said:
First, the equation can be simplified somewhat by substituting other variables for x and y, X and Y say. Can you see how a substitution for y simplifies both terms it occurs in?
Having done that, you could write a sequence of approximations for Y in terms of X, giving Y as an infinite sequence of functions of X.
- #5
- 2,009
- 974
When looking for ways to simplify it, think about what multiplying or adding logarithms do.
- #6
William Crawford
- 41
- 36
It is possible to express ##y## in terms of ##x##. From your calculations you have that
$$y^{-2}e^{y^2} = e^{x^2},$$
this it great. Rearrange the equation to look like
$$-y^2e^{-y^2} = -e^{-x^2}.$$
This is an equation of the form ##we^w = z## and can thus be solved using the Lambert ##W## function <LINK>. Accordingly
$$-y^2 = W_0\big(-e^{-x^2}\big) \qquad\vee\qquad -y^2 = W_{-1}\big(-e^{-x^2}\big),$$
provided that ##\vert x\vert\geq1##. Finally, note that both ##W_{-1}## and ##W_0## are negative valued for ##\vert x\vert\geq1##. Thus
$$ y = \pm\sqrt{-W_{k}\big(-e^{-x^2}\big)},\quad k =-1,0\ \text{and}\ \vert x\vert\geq1.$$
UPDATE
Thought I would include a plot of the solution as well.
The red curve corresponds to the solution ##y = \sqrt{-W_{-1}\big(-e^{-x^2}\big)}##.
The green curve corresponds to the solution ##y = -\sqrt{-W_{-1}\big(-e^{-x^2}\big)}##.
The blue curve corresponds to the solution ##y = \sqrt{-W_{0}\big(-e^{-x^2}\big)}##.
The magenta curve corresponds to the solution ##y = -\sqrt{-W_{0}\big(-e^{-x^2}\big)}##.
$$y^{-2}e^{y^2} = e^{x^2},$$
this it great. Rearrange the equation to look like
$$-y^2e^{-y^2} = -e^{-x^2}.$$
This is an equation of the form ##we^w = z## and can thus be solved using the Lambert ##W## function <LINK>. Accordingly
$$-y^2 = W_0\big(-e^{-x^2}\big) \qquad\vee\qquad -y^2 = W_{-1}\big(-e^{-x^2}\big),$$
provided that ##\vert x\vert\geq1##. Finally, note that both ##W_{-1}## and ##W_0## are negative valued for ##\vert x\vert\geq1##. Thus
$$ y = \pm\sqrt{-W_{k}\big(-e^{-x^2}\big)},\quad k =-1,0\ \text{and}\ \vert x\vert\geq1.$$
UPDATE
Thought I would include a plot of the solution as well.
The red curve corresponds to the solution ##y = \sqrt{-W_{-1}\big(-e^{-x^2}\big)}##.
The green curve corresponds to the solution ##y = -\sqrt{-W_{-1}\big(-e^{-x^2}\big)}##.
The blue curve corresponds to the solution ##y = \sqrt{-W_{0}\big(-e^{-x^2}\big)}##.
The magenta curve corresponds to the solution ##y = -\sqrt{-W_{0}\big(-e^{-x^2}\big)}##.
Last edited:
- #7
- 42,802
- 10,495
... though whether it constitutes a closed form solution is a matter of taste.William Crawford said:
- #8
William Crawford
- 41
- 36
I agree.haruspex said:
- #9
epenguin
Science Advisor
- 3,637
- 1,013
Yeah I was going to say.
What we have here is, let's say, a relation between ##x## and ##y##. We can write that ##y=f(x)## . By definition then ##x=f^{-1}\left( y\right)## and we call ##f^{-1}## the inverse of ##f##. We are used to plotting ##x## against ##y##; given ##x## we can then read off ##y##. But just as easily, given ##y## we can read ##x## off the same graph.
What happens is that years of school etc training tend to brainwash us into the habit of explicitly calculating the inverse function, i.e. given ##y## calculate ##x##, I.e. invert the function. which might be a logical thing to do in some cases but not in the following:
when there is no way to do it, i.e. no known inverse function;
when there might be a way to do it but you don't know what it is and it would be long to find out;
when there is a way of doing it, but it is so complicated that is not worth it; when the formula for the solution so to say does not speak to you, the way that simple enough formulae do.
If the problem is knowing ##y## find ##x##, graphically this is nothing new as explained above. Numerically, many scientific calculators or function plotters have routines which if you can calculate any function, can calculate its inverse to all accuracy you are likely to need.
In the present case we could say we have a relationship between two variables we can call ##x^{2}## and ##y^{2}##. ##x^{2}## ≥ 0 but ##y^{2}##≥ 1. To every value of ##x^{2}## corresponds one value of ##y^{2}##, but to every value of ##y^{2}## corresponds two of ##x^{2}##, see fig 1. Simples.
If we want it as function of ##x## itself see fig 2.
So a qualitative answer to the question is that to every y ≥ 1 corresponds four values of x in the form ± x1, ± x2
At risk of belaboring the obvious, when you have Y=X2 and you write X= ±√Y and say you have solved something, you haven't, you haven't done anything except show you know the special symbol for the inverse of squaring. The mathematical substance lies in the fact you know how to calculate that. Don't you?
This Lambert function does come up in some applications e.g. in enzyme kinetics, so it is good to know about the implementation mentioned by W Crawford.
For negative ##y## most of us might not want to get into ##ln## of negative numbers so I think that those two figs. sufficient.
What we have here is, let's say, a relation between ##x## and ##y##. We can write that ##y=f(x)## . By definition then ##x=f^{-1}\left( y\right)## and we call ##f^{-1}## the inverse of ##f##. We are used to plotting ##x## against ##y##; given ##x## we can then read off ##y##. But just as easily, given ##y## we can read ##x## off the same graph.
What happens is that years of school etc training tend to brainwash us into the habit of explicitly calculating the inverse function, i.e. given ##y## calculate ##x##, I.e. invert the function. which might be a logical thing to do in some cases but not in the following:
when there is no way to do it, i.e. no known inverse function;
when there might be a way to do it but you don't know what it is and it would be long to find out;
when there is a way of doing it, but it is so complicated that is not worth it; when the formula for the solution so to say does not speak to you, the way that simple enough formulae do.
If the problem is knowing ##y## find ##x##, graphically this is nothing new as explained above. Numerically, many scientific calculators or function plotters have routines which if you can calculate any function, can calculate its inverse to all accuracy you are likely to need.
In the present case we could say we have a relationship between two variables we can call ##x^{2}## and ##y^{2}##. ##x^{2}## ≥ 0 but ##y^{2}##≥ 1. To every value of ##x^{2}## corresponds one value of ##y^{2}##, but to every value of ##y^{2}## corresponds two of ##x^{2}##, see fig 1. Simples.
If we want it as function of ##x## itself see fig 2.
So a qualitative answer to the question is that to every y ≥ 1 corresponds four values of x in the form ± x1, ± x2
At risk of belaboring the obvious, when you have Y=X2 and you write X= ±√Y and say you have solved something, you haven't, you haven't done anything except show you know the special symbol for the inverse of squaring. The mathematical substance lies in the fact you know how to calculate that. Don't you?
This Lambert function does come up in some applications e.g. in enzyme kinetics, so it is good to know about the implementation mentioned by W Crawford.
For negative ##y## most of us might not want to get into ##ln## of negative numbers so I think that those two figs. sufficient.
Last edited:
Similar threads
- · Replies 26 ·
- · Replies 8 ·
- · Replies 17 ·
- · Replies 1 ·
- · Replies 18 ·
- · Replies 3 ·
- · Replies 5 ·