SaltMiner
- 6
- 3
- Homework Statement
- I think an old lecture note problem on refraction is wrong and I am right.
- Relevant Equations
- none (I think) although the general solution would involve Snell's Law.
I recently had some trouble understanding refraction but after I finally understood where I went wrong (thanks to the people on this forum) I went back to my old lecture notes because I thought that what I recently learned didn't fit right with something that had previously been presented in my introductory to physics course. Here it is:
"You are standing waist deep in the sea on a calm day and spot something shiny that seems to be 1 metre ahead of you. Where actually is this shiny thing?"
Assumptions:
Calm water (smooth surface)
Sea floor is level
Height = 1.78m
Waist = half of height
n_air = 1
n_water = 1.33
Now my problem isn't in working out the answer because that whole process was presented in the lecture power point. My problem is that I thought that when refraction occurred in such a scenario as this, where the object appears to be should be directly above where it actually is. That is to say, there is no horizontal change in distance, only vertical due to refraction.
So, the image given was this:
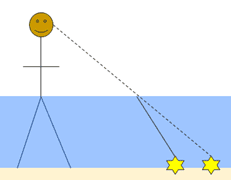
But what I think it should have been is this:
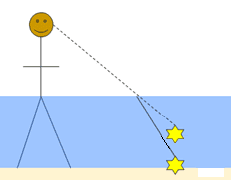
So if I am right in this, then the question was wrong to begin with. The object should still be 1 meter away from you, or if it actually is closer to you, it should appear that way as well.
Am I correct in this? Thanks.
"You are standing waist deep in the sea on a calm day and spot something shiny that seems to be 1 metre ahead of you. Where actually is this shiny thing?"
Assumptions:
Calm water (smooth surface)
Sea floor is level
Height = 1.78m
Waist = half of height
n_air = 1
n_water = 1.33
Now my problem isn't in working out the answer because that whole process was presented in the lecture power point. My problem is that I thought that when refraction occurred in such a scenario as this, where the object appears to be should be directly above where it actually is. That is to say, there is no horizontal change in distance, only vertical due to refraction.
So, the image given was this:
But what I think it should have been is this:
So if I am right in this, then the question was wrong to begin with. The object should still be 1 meter away from you, or if it actually is closer to you, it should appear that way as well.
Am I correct in this? Thanks.