A Help with Discrete Sine Transform

[kaniello]

Hi,
I am a neophyte in Discrete Fourier Transform and I am procticing with discrete Sine-transform.
Specifically I want to calculate $$ \mathcal{F}_s \lbrace x \cdot e^{-x^2} \rbrace = \int\limits_{0}^{\infty } x \cdot e^{-x^2} \cdot \sin\left(x\right)\, \mathrm{d}x
= \frac{1}{2} \pi^2 \omega e^{- \frac{1}{4} \pi^2 \omega^2} $$
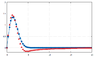
I am using the FFTw library and with a 64 points I get a very poor result. Can anybody please help to improve it?
This is my C++ code, plot and numerical data are attached.
Thank you very much in advance

 

[scottdave]

I don't see any attachments.
Your itex "command is not working as you intend to produce laTex. I think you should use double number-signs, before and after. I think this is what you want.
$$ \mathcal{F}_s \lbrace x \cdot e^{-x^2} \rbrace = \int\limits_{0}^{\infty } x \cdot e^{-x^2} \cdot \sin\left(x\right)\, \mathrm{d}x
= \frac{1}{2} \pi^2 \omega e^{- \frac{1}{4} \pi^2 \omega^2} $$

You can always click the preview button before posting a message. There is a latex help guide available. https://www.physicsforums.com/help/latexhelp/

 

[kaniello]

Hello Scottdave,
thank you very much for your hint, my post looks definitely better now.
I hope that you can see the attachments now

 

[mathman]

Your original equation has a typo (sin(?)). It would be helpful to give more information about the graphs - which is which?

 

[kaniello]

Hi mathman,
the original equation is $$ f(x) = x \cdot e^{-x^2}$$ . Its analytical sine-transform is given by
$$ \mathcal{F}_s \lbrace f(x) \rbrace (\omega) = \int\limits_{0}^{\infty } x \cdot e^{-x^2} \cdot \sin\left(x\right)\, \mathrm{d}x
= \frac{1}{2} \pi^2 \omega e^{- \frac{1}{4} \pi^2 \omega^2}$$
I uploaded the plot again with a legend

 

[mathman]

I presume the argument for the sin is ωx. I suspect that you need a finer mesh for the Fourier transform for small ω.

 

[scottdave]

I presume the argument for the sin is ωx. I suspect that you need a finer mesh for the Fourier transform for small ω.

It has been awhile since I have done these, but I was kind of wondering how the ω just popped in when it is not in the integral.

 

[kaniello]

Sorry for the typing error,of course the the correct argument $$\sin \left(\omega x \right)$$. The resolution is still poor even with 256 points Can anybody tell me where the deviation between 2.0 and 7.0 comes from? (please see attachments).

 

[I like Serena]

Hi kaniello,

There seems to be a bit of a mixup with factors pi.
W|A (link) reports the sine transform to be:
$$\mathscr F_s\{xe^{-x^2}\}(\omega) = \frac 1{2\sqrt 2}\omega e^{-\frac 14 \omega^2}$$
Of course we can have a different normalization constant than the one given, but not a different argument to the exponential function.

Anyway, if I do a discrete Fourier transform on the data, I don't get the dip that you're seeing between 2 and 7.
So it appears there is something wrong with that FFTW routine that you're using.
Unfortunately I'm not familiar with it.

I do notice that the dip might be explained if the cosine transform somehow crept in - that one does have a dip between 2 and 7.
And I guess it might also be caused by a filter (window function) that is applied before applying the FFT.
Have you tried using an FFT routine from a different library?

 

[kaniello]

Dear I like Serena,
thanks a lot for your reply.

Which library did you use to perform the sine transform of $xe^{-x^2}$ ? It would be really interesting to compare the results.

I do not apply any filter to my Input data but I will try to understand from the FFTw Website if it is somehow executed automatically

 

[I like Serena]

You're welcome.
I didn't use any library - for a quick check I just used Excel's built in Fourier transform (one of the Data Analysis Tools).

 

[scottdave]

Hello @kaniello . I just thought I would add some information for you, since you did state you are new to Discrete Fourier Transforms.
Are you aware of how sampling frequency affects the ability to regain the original signal? Every time varying signal is composed of various sinusoidal frequencies.
For the highest frequency in the time varying signal, you must sample at a rate at least twice of that frequency.

You may find this Wikipedia article helpful, to start. https://en.wikipedia.org/wiki/Nyquist_frequency

In real-world digital signal processing, we want to make sure that we are sampling at a high enough frequency. That is why a low pass filter is used on the signal before sampling - to filter out the higher frequencies that can lead to "aliasing".