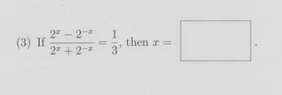SUMMARY
The forum discussion focuses on solving the exponential equation $$\frac{2^x - 2^{-x}}{2^x + 2^{-x}} = \frac{1}{3}$$. Participants detail the steps to manipulate the equation, including cross-multiplication and substitution with $$u = 2^x$$. The solution leads to the conclusion that $$x = \frac{1}{2}$$, while also addressing the rejection of negative solutions due to the nature of exponential functions. The discussion emphasizes the importance of proper algebraic manipulation and understanding exponential properties.
PREREQUISITES
- Understanding of exponential functions and their properties
- Familiarity with algebraic manipulation techniques
- Knowledge of solving quadratic equations
- Ability to perform cross-multiplication in equations
NEXT STEPS
- Study the properties of exponential functions, particularly $$2^x$$
- Learn techniques for solving rational equations
- Explore quadratic equation solving methods, including factoring and the quadratic formula
- Investigate the implications of negative solutions in exponential equations
USEFUL FOR
Mathematics students, educators, and anyone interested in mastering exponential equations and algebraic manipulation techniques.