Help with, I am sure, a really simple circular motion problem

[Nathi ORea]

Summary: I am just trying to go through a Brilliant physics unit. I came across this axe throwing question which I don't get at all how they get the answer.

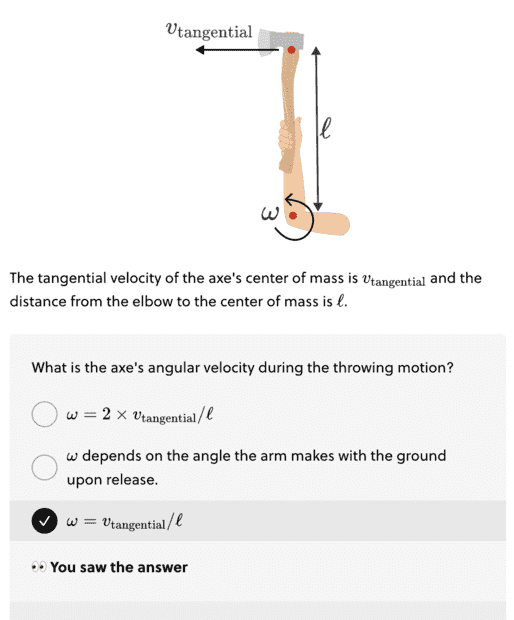
You can see the answer there.

So their explanation is;

'In going around the circle, the red point moves through an angle of
θ = 360° or θ = 2π, and its angular velocity is simply ω = θ/T'

Now I actually thought that would be the answer.. Just 2πl/T, but they continue

'ω = θ/T
= 2π X v(tangential)/l
= v(tangential/l'

I guess I am stuck on how they got from ω = θ/T to ω = 2π X v(tangential)/l

I can see how they simplified ω = 2π X v(tangential)/l to ω = v(tangential/l'

I am just doing this Brilliant course because I find it interesting and want to learn more about how our world works. I am certainly no maths wiz.. lol. but I appreciate any help.

 

[anuttarasammyak]

$$\omega=\frac{\theta}{T}$$
$$=\frac{\theta l}{T l}=\frac{\frac{\theta l}{T}}{l}=\frac{v}{l}$$

 

[Nathi ORea]

$$\omega=\frac{\theta}{T}$$
$$=\frac{\theta l}{T l}=\frac{\frac{\theta l}{T}}{l}=\frac{v}{l}$$

Thanks for replying.
I think I know why you put an ‘l’ next to theta (because that gives you the actual distance around the circle) but why does T have an ‘l’.

I feel so dumb…lol

 

[anuttarasammyak]

As a math rule
$$\frac{a}{b}=\frac{al}{bl}$$
Multiplying a same number to numerator and denominator does not alter the number.

 

[Chestermiller]

$2\pi l=v_{tangential}T=circumference\ of\ circle$, where T is the period of rotation. So, $$T=\frac{2\pi l}{v_{tangential}}$$

 

[Lnewqban]

Please, see:
http://hyperphysics.phy-astr.gsu.edu/hbase/rotq.html#rq

http://hyperphysics.phy-astr.gsu.edu/hbase/shm.html#c1

 

[Nathi ORea]

Please, see:
http://hyperphysics.phy-astr.gsu.edu/hbase/rotq.html#rq

http://hyperphysics.phy-astr.gsu.edu/hbase/shm.html#c1

Thanks for that. I misunderstood what 'angular velocity' actually meant.

I have been trying to work it out, but the whole angular velocity and radians thing is not coming very intuitively to me at all... lol

 

[Lnewqban]

Thanks for that. I misunderstood what 'angular velocity' actually meant.

I have been trying to work it out, but the whole angular velocity and radians thing is not coming very intuitively to me at all... lol

You are welcome.
One full turn per second equals 6.28... radians/second.