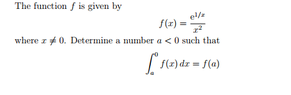Help with Integral Problem: Tips to Get Started

[Samme013]

View attachment 3410

Ok so i am stuck on this problem , i tried substituting 1/x for u did not help , tried turning it into a limit where the top integration limit would be c and c-->0 did not get anywhere.Also tried substituting f(x) for its anti derivative [-e1/x] with no luck.So yeah at least some tips to get me started would be much appreciated.

 

[chisigma]

https://www.physicsforums.com/attachments/3410

Ok so i am stuck on this problem , i tried substituting 1/x for u did not help , tried turning it into a limit where the top integration limit would be c and c-->0 did not get anywhere.Also tried substituting f(x) for its anti derivative [-e1/x] with no luck.So yeah at least some tips to get me started would be much appreciated.

Wellcome on MHB Samme013!...

... the substitution $\displaystyle \frac{1}{x} = t$ may be useful because...

$\displaystyle \frac{1}{x} = t \implies x= \frac{1}{t} \implies d x = - \frac{d t}{t^{2}} \implies \int \frac{e^{\frac{1}{x}}} {x^{2}}\ d x = - \int e^{t}\ d t\ (1)$

Kind regards

$\chi$ $\sigma$

 

[Samme013]

Wellcome on MHB Samme013!...

... the substitution $\displaystyle \frac{1}{x} = t$ may be useful because...

$\displaystyle \frac{1}{x} = t \implies x= \frac{1}{t} \implies d x = - \frac{d t}{t^{2}} \implies \int \frac{e^{\frac{1}{x}}} {x^{2}}\ d x = - \int e^{t}\ d t\ (1)$

Kind regards

$\chi$ $\sigma$

Thanks !, i tried that but i get the following:
$\ \lim_{{c}\to{\infty}} \int_{c}^{1/a} \,e^t dt = f(a)=\lim_{{c}\to{\infty}} e^(1/a) - e^c $

Which is just -infinity and does not help me find a

 

[MarkFL]

Try differentiating the integral equation given with respect to $a$...this leads to a quadratic in $a$, for which you discard the positive root.

 

[Samme013]

Try differentiating the integral equation given with respect to $a$...this leads to a quadratic in $a$, for which you discard the positive root.

Awesome , i took the partial derivative with respect to a on both sides and got two answers , 1 posiive , a = $\sqrt{2} - 1$ is that right?

 

[MarkFL]

Awesome , i took the partial derivative with respect to a on both sides and got two answers , 1 posiive , a = $\sqrt{2} - 1$ is that right?

You should obtain:

$$a^2-2a-1=0$$

You want the negative root ($a<0$), which is $$a=1-\sqrt{2}$$

 

[Samme013]

You should obtain:

$$a^2-2a-1=0$$

You want the negative root ($a<0$), which is $$a=1-\sqrt{2}$$

Derp yeah thought a was positive , that was the other root i got , thanks !

 

[Samme013]

You should obtain:

$$a^2-2a-1=0$$

You want the negative root ($a<0$), which is $$a=1-\sqrt{2}$$

Just tried something else and got a different answer:
by substituting u= 1/x and if we get :
$ f(a) = \int_{-\infty}^{1/a} \,d e^t ft = e^(1/a) = [e^(1/a)]/a^2]$ ... a = 1 or a = -1 so a = -1.
Did i do something wrong or is it not possible to take partial derivatives like we did before since a is a contant?

 

[MarkFL]

I'm not following what you did there, can you restate it?

 

[Samme013]

I'm not following what you did there, can you restate it?

for u=1/x , du=-1/x^2 dx so substituting into the given integral and changing the integration limits sice x=a -> u=1/a and when x-->0 u--->-infiniy since x approaches 0 from the left sice in the given integral a is the other integration limit and is negative so:

$f(a)=-\int_{1/a}^{-\infty} \, e^u du =- \lim_{{c}\to{-\infty}} \int_{1/a}^{c} \, e^t dt = \lim_{{c}\to{-\infty}} -e^c +e^(1/a)=e^(1/a)=f(a)=[e^(1/a)]/a^2] $
so solving the equation for a a =1 or a = -1 so we keep a = -a <0

 

[MarkFL]

for u=1/x , du=-1/x^2 dx so substituting into the given integral and changing the integration limits sice x=a -> u=1/a and when x-->0 u--->-infiniy since x approaches 0 from the left sice in the given integral a is the other integration limit and is negative so:

$f(a)=-\int_{1/a}^{-\infty} \, e^u du =- \lim_{{c}\to{-\infty}} \int_{1/a}^{c} \, e^t dt = \lim_{{c}\to{-\infty}} -e^c +e^(1/a)=e^(1/a)=f(a)=[e^(1/a)]/a^2] $
so solving the equation for a a =1 or a = -1 so we keep a = -a <0

Okay, if you try the substitution:

$$u=\frac{1}{x}\,\therefore\,du=-\frac{1}{x^2}$$

Then, the integral becomes:

$$\int_{\infty}^{\frac{1}{a}}e^u\,du$$

You have incorrectly changed the limits of integration...since:

$$u(x)=\frac{1}{x}$$

We find:

$$u(0)=\infty\,u(a)=\frac{1}{a}$$

Trying to evaluate the resulting improper integral above does not result in a converging value. This is why I suggested using differentiation.