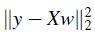SUMMARY
This discussion centers on understanding mathematical notation in the context of Machine Learning, specifically the squared 2-norm and its application in minimizing the Euclidean length of a vector. The notation ##\mathbf b = \mathbf{y - Xw}## is introduced, leading to the formulation of the Normal Equations for ordinary least squares estimations. The conversation emphasizes the importance of consistent notation, recommending the book "Learning From Data" as a foundational resource for self-learners in Machine Learning.
PREREQUISITES
- Understanding of linear algebra concepts, particularly vectors and matrices.
- Familiarity with ordinary least squares (OLS) regression techniques.
- Basic knowledge of Machine Learning principles and terminology.
- Ability to interpret mathematical notation commonly used in statistics and data analysis.
NEXT STEPS
- Study the Normal Equations in the context of ordinary least squares regression.
- Learn about the properties and applications of the squared 2-norm in optimization problems.
- Explore the book "Learning From Data" and its associated resources for a structured approach to Machine Learning.
- Research the differences between various mathematical notations used in statistics and Machine Learning literature.
USEFUL FOR
Students and professionals in Machine Learning, data scientists, and anyone seeking to clarify mathematical notation and concepts related to regression analysis and optimization techniques.